题目内容
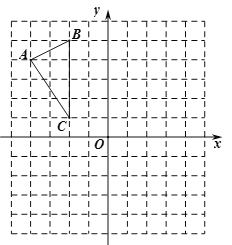
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.

(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
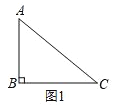
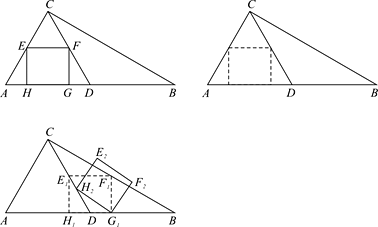
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
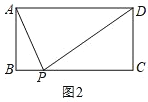
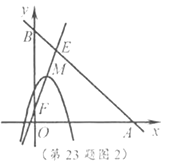
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .(3)①当
.(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】(1)写出点![]() 的坐标,代入直线
的坐标,代入直线![]() 进行判断即可.
进行判断即可.
(2)直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,求出点
,求出点![]() 坐标,把
坐标,把![]() 在抛物线上,代入求得
在抛物线上,代入求得![]() ,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出
,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]() ,联立方程组
,联立方程组![]() ,得
,得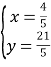 .点
.点![]() ,
,![]() .分三种情况进行讨论.
.分三种情况进行讨论.
【解答】
(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
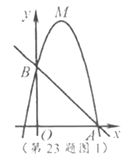
(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得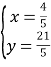 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.

练习册系列答案
相关题目