Question

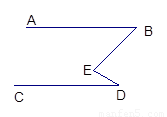
已知：如图，ＡＢ、ＢＥ、ＥＤ、ＣＤ依次相交于Ｂ、Ｅ、Ｄ，∠Ｅ＝∠Ｂ＋∠Ｄ.

试说明ＡＢ∥ＣＤ.

 

Answer 1

【答案】

见解析

【解析】

试题分析：过E作EF∥AB，则得到∠BEF=∠B，因为∠E=∠BEF+∠DEF=∠B+∠DEF，已知∠E=∠B+∠D，则得到∠DEF=∠D，满足关于EF，CD平行的条件：内错角相等，两直线平行．根据两条直线分别平行于第三条直线，那么这两条直线平行，所以AB∥CD．

过E作EF∥AB；

∴∠BEF=∠B；

∵∠E=∠BEF+∠DEF=∠B+∠DEF，且∠E=∠B+∠D，

∴∠DEF=∠D；

∴EF∥CD；

∴AB∥CD．

考点：本题考查的是平行线的判定

点评：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．