Question

【题目】如图，等边△ABC的边长为12cm，点P、Q分别是边BC、CA上的动点，点P、Q分别从顶点B、C同时出发，且它们的速度都为3cm/s．

（1）如图1，连接PQ，求经过多少秒后，△PCQ是直角三角形；

（2）如图2，连接AP、BQ交于点M，在点P、Q运动的过程中，∠AMQ的大小是否变化？若变化，请说明理由；若不变，请求出它的度数．

Answer 1

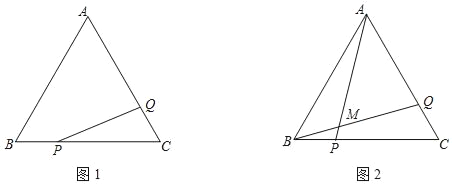
【答案】（1）经过秒或秒，△PCQ是直角三角形（2）∠AMQ的大小不变

【解析】

（1）分两种情形分别求解即可解决问题；

（2）由△AB≌△BCQ（SAS），推出∠BAP＝∠CBQ，可得∠AMQ＝∠PAB+∠ABQ＝∠CBQ+∠ABQ＝∠ABC＝60°即可．

（1）设经过t秒后，△PCQ是直角三角形．

由题意：PC＝（12﹣3t）cm，CQ＝3t，

∵△ABC是等边三角形，

∴∠C＝60°，

当∠PQC＝90°时，∠QPC＝30°，

∴PC＝2CQ，

∴12﹣3t＝6t，

解得t＝；

当∠QPC＝90°时，∠PQC＝30°，

∴CQ＝2PC，

∴3t＝2（12﹣3t），

解得t＝，

∴经过秒或秒，△PCQ是直角三角形；

（2）结论：∠AMQ的大小不变．

∵△ABC是等边三角形，

∴AB＝BC，∠ABC＝∠C＝60°，

∵点P，Q的速度相等，

∴BP＝CQ，

在△ABP和△BCQ中，

，

∴△AB≌△BCQ（SAS），

∴∠BAP＝∠CBQ，

∴∠AMQ＝∠PAB+∠ABQ＝∠CBQ+∠ABQ＝∠ABC＝60°．