题目内容
【题目】点D是△ABC中∠BAC的平分线和BC的垂直平分线的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
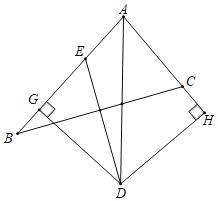
(1)求证:BG=CH;
(2)若AB=12,AC=6,则BG= .
【答案】(1)见解析;(2)3
【解析】
(1)连接BD、CD,根据线段垂直平分线的性质可得DB=DC;依据角平分线的性质可得DG=DH;依据HL定理可判断出Rt△BDG≌Rt△CDH,根据全等三角形的性质即可得出结论;
(2)由Rt△ADG≌Rt△ADH(HL),得出AG=AH,进而得出答案.
(1)证明:如图,连接BD、CD,
∵D是线段BC垂直平分线上的点,
∴BD=DC,
∵D是∠BAC平分线上的点,DG⊥AB,DH⊥AC
∴DG=DH,∠DGB=∠H=90°,
在Rt△BDG和Rt△CDH中,![]() ,
,
∴Rt△BDG≌Rt△CDH(HL),
∴BG=CH;

(2)解:∵在Rt△ADG与Rt△ADH中,
![]()
Rt△ADG≌Rt△ADH(HL),
∴AG=AH,
∴AB﹣AC=AG+BG﹣(AH﹣CH)=2BG=12﹣6=6,
∴NG=3;
故答案为:3.

练习册系列答案
相关题目
【题目】某校积极开展“我爱我的祖国”教育知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其预赛成绩如图所示:
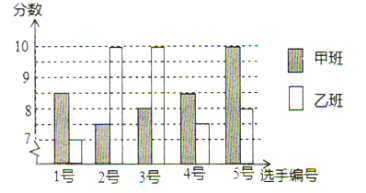
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.