题目内容
 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,连接BD,CD.
(1)求证:BD=CD;
(2)若∠ABC的平分线交AD于点E,求证:CD=DE.
 证明:(1)∵AD为直径,AD⊥BC,
证明:(1)∵AD为直径,AD⊥BC,∴
 ,
,∴BD=CD.
(2)∵
 ,
,∴∠BAD=∠CBD,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBE,
∵∠DBE=∠CBE+∠CBD,∠BED=∠ABE+∠BAD,
∴∠BAD+∠ABE=∠CBD+∠EBF,
即∠BED=∠EBD,
∴BD=DE,
∴CD=DE.
分析:(1)根据垂径定理以及圆心角与所对弦的关系,直接得出答案即可;
(2)利用角平分线的性质以及等腰三角形的性质即可得出BD=DE,即可得出答案.
点评:此题主要考查了圆周角定理以及垂径定理和角平分线的性质,根据已知得出∠DBE=∠BED是解题关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
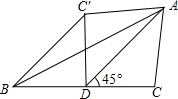 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.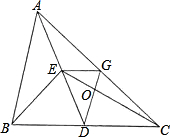 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.