题目内容
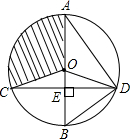 如图,在⊙O中,已知点E是直径AB上一动点,过点E作弦CD⊥AB,OD=5.
如图,在⊙O中,已知点E是直径AB上一动点,过点E作弦CD⊥AB,OD=5.(1)若弦CD平分半径OB,求CD的长;
(2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留π).
分析:(1)在直角三角形ODE中用勾股定理求出DE的长,然后确定CD的长.(2)根据∠ADO:∠EDO=4:1,而∠OAD=∠ADO,∠OAD+∠ADO+∠EDO=90°,可以求出∠EDO的度数,得到∠AOD的度数,就求出了∠AOC的度数,然后利用扇形面积公式求出阴影部分的面积.
解答:解:(1)在直角△ODE中:OD=5,OE=
,
∴DE=
=
=
.
∴CD=2DE=5
;
(2)设∠EDO=x°,则∠ADO=∠OAD=4x°,
在直角△AED中,∠EAD+∠ADE=90°,
即:4x+4x+x=90
∴x=10°.
∴∠AOC=∠AOD=90°+10°=100°.
∴S阴影=
=
.
| 5 |
| 2 |
∴DE=
| OD2-OE2 |
25-
|
5
| ||
| 2 |
∴CD=2DE=5
| 3 |
(2)设∠EDO=x°,则∠ADO=∠OAD=4x°,
在直角△AED中,∠EAD+∠ADE=90°,
即:4x+4x+x=90
∴x=10°.
∴∠AOC=∠AOD=90°+10°=100°.
∴S阴影=
| 100•π•52 |
| 360 |
| 125π |
| 18 |
点评:本题考查的是扇形面积的计算,(1)根据垂径定理得到CE=DE,然后在直角三角形OED中用勾股定理求出ED的长,再确定CD的长.(2)根据题意求出∠AOC的度数,然后用扇形面积公式求出阴影部分的面积.

练习册系列答案
相关题目
 22、如图,在△ABC中,已知B(-3,1).
22、如图,在△ABC中,已知B(-3,1). 9、如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点D,过D点作EF∥BC,交AB于点E,交AC于点F,若BE+CF=9,则线段EF的长为( )
9、如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点D,过D点作EF∥BC,交AB于点E,交AC于点F,若BE+CF=9,则线段EF的长为( ) 17、如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是
17、如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是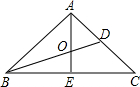 如图,在△ABC中,已知AB=AC=10,BC=16,O是△ABC的重心,则tan∠DBC的值是
如图,在△ABC中,已知AB=AC=10,BC=16,O是△ABC的重心,则tan∠DBC的值是 如图,在△ABC中,已知AB=AC,D为AB上一点,且AD=CD=BC,则∠B=
如图,在△ABC中,已知AB=AC,D为AB上一点,且AD=CD=BC,则∠B=