题目内容
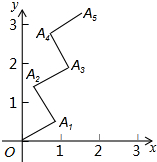 (2012•威海)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为
(2012•威海)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为(503
-503,503
+503)
| 3 |
| 3 |
(503
-503,503
+503)
.| 3 |
| 3 |
分析:过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,然后求出点A1的坐标,以及A1C、A2C的长度,并出A2、A3、A4、A5、A6的坐标,然后总结出点的坐标的变化规律,再把2012代入规律进行计算即可得解.
解答: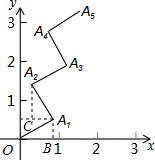 解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,
解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,
∵OA1=1,OA1与x轴的夹角为30°,
∴OB=OA1•cos30°=1×
=
,
A1B=OA1•sin30°=1×
=
,
∴点A1的坐标为(
,
),
∵A2A1⊥OA1,OA1与x轴的夹角为30°,
∴∠OA1C=30°,∠A2A1C=90°-30°=60°,
∴∠A1A2C=90°-60°=30°,
同理可求:A2C=OB=
,A1C=A1B=
,
所以,点A2的坐标为(
-
,
+
),
点A3的坐标为(
-
+
,
+
+
),即(
-
,
+1),
点A4的坐标为(
-
-
,
+1+
),即(
-1,
+1),
点A5的坐标为(
-1+
,
+1+
),即(
-1,
+
),
点A6的坐标为(
-1-
,
+
+
),即(
-
,
+
),
…,
当n为奇数时,点An的坐标为(
-
,
+
),
当n为偶数时,点An的坐标为(
-
,
+
),
所以,当n=2012时,
-
=503
-503,
+
=503
+503,
点A2012的坐标为(503
-503,503
+503).
故答案为:(503
-503,503
+503).
 解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,
解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,∵OA1=1,OA1与x轴的夹角为30°,
∴OB=OA1•cos30°=1×
| ||
| 2 |
| ||
| 2 |
A1B=OA1•sin30°=1×
| 1 |
| 2 |
| 1 |
| 2 |
∴点A1的坐标为(
| ||
| 2 |
| 1 |
| 2 |
∵A2A1⊥OA1,OA1与x轴的夹角为30°,
∴∠OA1C=30°,∠A2A1C=90°-30°=60°,
∴∠A1A2C=90°-60°=30°,
同理可求:A2C=OB=
| ||
| 2 |
| 1 |
| 2 |
所以,点A2的坐标为(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点A3的坐标为(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
点A4的坐标为(
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
点A5的坐标为(
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 2 |
点A6的坐标为(
3
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
…,
当n为奇数时,点An的坐标为(
| n+1 |
| 4 |
| 3 |
| n-1 |
| 4 |
| n-1 |
| 4 |
| 3 |
| n+1 |
| 4 |
当n为偶数时,点An的坐标为(
| n |
| 4 |
| 3 |
| n |
| 4 |
| n |
| 4 |
| 3 |
| n |
| 4 |
所以,当n=2012时,
| n |
| 4 |
| 3 |
| n |
| 4 |
| 3 |
| n |
| 4 |
| 3 |
| n |
| 4 |
| 3 |
点A2012的坐标为(503
| 3 |
| 3 |
故答案为:(503
| 3 |
| 3 |
点评:本题考查了点的坐标的规律变化问题,作出辅助线,求出各点的横坐标与纵坐标的规律变化的数值,然后依次写出前几个点的坐标,根据坐标与点的序号的特点找出点的坐标的通式是解题的关键.

练习册系列答案
相关题目
 (2012•威海)如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为( )
(2012•威海)如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为( ) (2012•威海)如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
(2012•威海)如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( ) (2012•威海)如图,直线l1,l2交于点A,观察图象,点A的坐标可以看作方程组
(2012•威海)如图,直线l1,l2交于点A,观察图象,点A的坐标可以看作方程组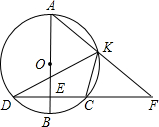 (2012•威海)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E.K为
(2012•威海)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E.K为