题目内容
点P(x-1,x+1)关于原点O的对称点P′不可能是
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
B
分析:由于x可取任意实数,而x-1=0时,x=1;x+1=0时,x=-1.分三种情况对P点的坐标进行讨论:①x≤-1;②-1<x≤1;③x>1.得出P点不可能在的象限,再根据关于原点对称的两点的坐标特点,选出正确选项.
解答:如果x-1=0,那么x=1;如果x+1=0,那么x=-1.
分三种情况对P点的坐标进行讨论:
①当x≤-1时,x-1<0,x+1≤0,此时P(x-1,x+1)在第三象限或x轴负半轴上;
②当-1<x≤1时,x-1≤0,x+1>0,此时P(x-1,x+1)在第二象限或y轴正半轴上;
③当x>1时,x-1>0,x+1>0,此时P(x-1,x+1)在第一象限.
即P点可能在第一、二、三象限,不可能在第四象限,
∵第四象限关于原点O的对称点在第二象限,
∴点P(x-1,x+1)关于原点O的对称点P′不可能在第二象限.
故选B.
点评:本题主要考查关于原点对称的两点的坐标特点:两点的横、纵坐标都是互为相反数.关键是将x的值进行正确分类,从而得出P点不可能在的象限,这也是本题的难点.
分析:由于x可取任意实数,而x-1=0时,x=1;x+1=0时,x=-1.分三种情况对P点的坐标进行讨论:①x≤-1;②-1<x≤1;③x>1.得出P点不可能在的象限,再根据关于原点对称的两点的坐标特点,选出正确选项.
解答:如果x-1=0,那么x=1;如果x+1=0,那么x=-1.
分三种情况对P点的坐标进行讨论:
①当x≤-1时,x-1<0,x+1≤0,此时P(x-1,x+1)在第三象限或x轴负半轴上;
②当-1<x≤1时,x-1≤0,x+1>0,此时P(x-1,x+1)在第二象限或y轴正半轴上;
③当x>1时,x-1>0,x+1>0,此时P(x-1,x+1)在第一象限.
即P点可能在第一、二、三象限,不可能在第四象限,
∵第四象限关于原点O的对称点在第二象限,
∴点P(x-1,x+1)关于原点O的对称点P′不可能在第二象限.
故选B.
点评:本题主要考查关于原点对称的两点的坐标特点:两点的横、纵坐标都是互为相反数.关键是将x的值进行正确分类,从而得出P点不可能在的象限,这也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
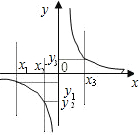 在函数y=
在函数y=| k |
| x |
| A、y1<0<y2 |
| B、y3<0<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
 9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为
9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为 23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.