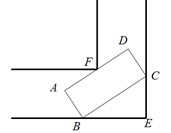
题目内容
如图,在直角坐标系中,点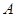 的坐标为
的坐标为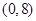 ,点
,点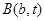 在直线
在直线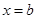 上运动,点
上运动,点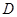 、
、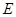 、
、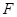 分别为
分别为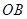 、
、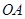 、
、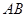 的中点,其中
的中点,其中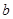 是大于零的常数.
是大于零的常数.
(1)请判断四边形 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)试求四边形 的面积
的面积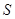 与
与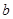 的关系式;
的关系式;
(3)设直线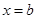 与
与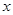 轴交于点
轴交于点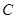 ,问:四边形
,问:四边形 能不能是矩形?若能,求出
能不能是矩形?若能,求出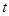 的值;若不能,说明理由.
的值;若不能,说明理由.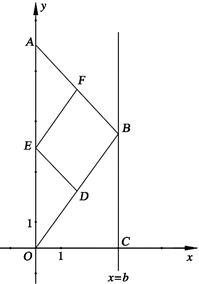
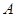 的坐标为
的坐标为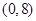 ,点
,点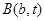 在直线
在直线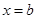 上运动,点
上运动,点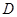 、
、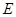 、
、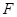 分别为
分别为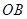 、
、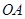 、
、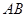 的中点,其中
的中点,其中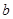 是大于零的常数.
是大于零的常数.(1)请判断四边形
 的形状,并证明你的结论;
的形状,并证明你的结论;(2)试求四边形
 的面积
的面积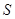 与
与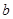 的关系式;
的关系式;(3)设直线
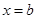 与
与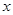 轴交于点
轴交于点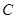 ,问:四边形
,问:四边形 能不能是矩形?若能,求出
能不能是矩形?若能,求出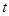 的值;若不能,说明理由.
的值;若不能,说明理由.
解:(1)四边形 是平行四边形.
是平行四边形.
证明:∵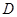 、
、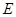 分别是
分别是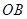 、
、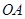 的中点
的中点
∴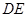 ∥
∥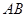
同理,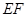 ∥
∥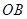
∴四边形 是平行四边形
是平行四边形
(2)解法一: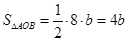
由(1)得: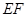 ∥
∥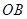
∴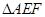 ∽
∽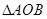
∴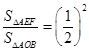 ∴
∴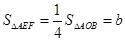
同理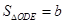
∴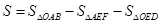
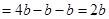 , 即
, 即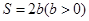
解法二:连结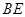 ,
,
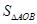 =
=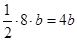
∵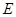 、
、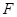 分别是
分别是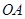 、
、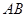 的中点
的中点
∴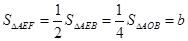
同理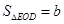
∴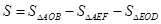
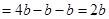 , 即
, 即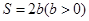
(3)解法一:以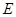 为圆心,
为圆心,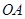 长为直径的圆记为⊙
长为直径的圆记为⊙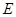 ,
,
① 当直线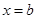 与⊙
与⊙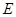 相切或相交时,若点
相切或相交时,若点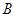 是交点或切点,则
是交点或切点,则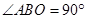 ,
,
由(1)知,四边形 是矩形.
是矩形.
此时0<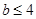 ,
,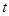 >0,可得
>0,可得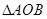 ∽
∽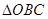
故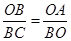 即
即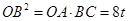
在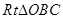 中,
中,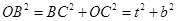 ∴
∴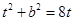 ∴
∴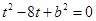 ,
,
解得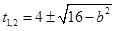
② 当直线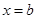 与⊙
与⊙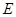 相离时,
相离时,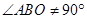 ,
,
∴四边形 不是矩形,此时
不是矩形,此时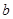 >4,
>4,
∴当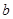 >4时,四边形
>4时,四边形 不是矩形
不是矩形
综上所述:当0<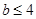 ,四边形
,四边形 是矩形,这时
是矩形,这时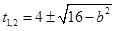 ;当
;当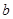 >4时,四边形
>4时,四边形 不是矩形.
不是矩形.
解法二:由(1)知:当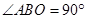 时,四边形
时,四边形 是矩形,
是矩形,
此时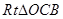 ∽
∽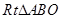 .
.
∴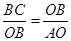 , 即
, 即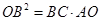
又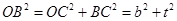 ,
,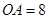
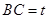
 ,
,
∴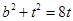
∴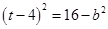
① 当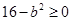 时,解得
时,解得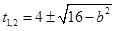 ,这时四边形
,这时四边形 是矩形.
是矩形.
② 当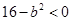 时,
时,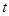 不存在,这时四边形
不存在,这时四边形 不是矩形.
不是矩形.
解法三:如图,过点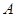 作
作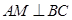 于点
于点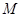 ,
,
在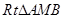 中,
中,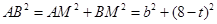
在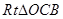 中,
中,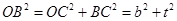
在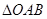 中,当
中,当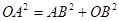 时,
时,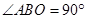 ,
,
则四边形 是矩形.
是矩形.
所以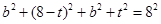
化简得: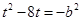
配方得: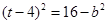
 是平行四边形.
是平行四边形. 证明:∵
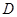 、
、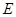 分别是
分别是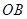 、
、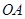 的中点
的中点∴
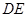 ∥
∥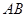
同理,
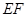 ∥
∥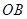
∴四边形
 是平行四边形
是平行四边形 (2)解法一:
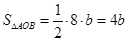
由(1)得:
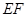 ∥
∥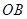
∴
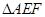 ∽
∽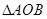
∴
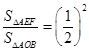 ∴
∴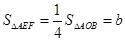
同理
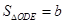
∴
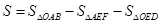
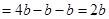 , 即
, 即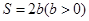
解法二:连结
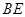 ,
,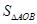 =
=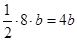
∵
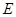 、
、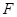 分别是
分别是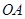 、
、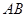 的中点
的中点∴
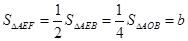
同理
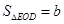
∴
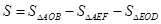
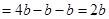 , 即
, 即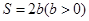
(3)解法一:以
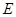 为圆心,
为圆心,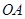 长为直径的圆记为⊙
长为直径的圆记为⊙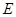 ,
, ① 当直线
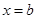 与⊙
与⊙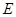 相切或相交时,若点
相切或相交时,若点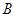 是交点或切点,则
是交点或切点,则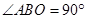 ,
,由(1)知,四边形
 是矩形.
是矩形. 此时0<
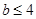 ,
,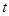 >0,可得
>0,可得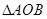 ∽
∽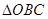
故
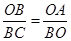 即
即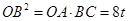
在
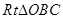 中,
中,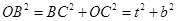 ∴
∴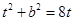 ∴
∴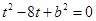 ,
,解得
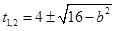
② 当直线
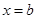 与⊙
与⊙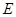 相离时,
相离时,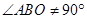 ,
,∴四边形
 不是矩形,此时
不是矩形,此时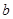 >4,
>4,∴当
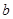 >4时,四边形
>4时,四边形 不是矩形
不是矩形综上所述:当0<
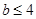 ,四边形
,四边形 是矩形,这时
是矩形,这时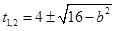 ;当
;当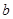 >4时,四边形
>4时,四边形 不是矩形.
不是矩形. 解法二:由(1)知:当
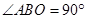 时,四边形
时,四边形 是矩形,
是矩形,此时
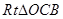 ∽
∽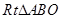 .
.∴
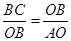 , 即
, 即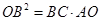
又
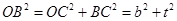 ,
,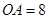
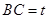
 ,
, ∴
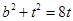
∴
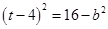
① 当
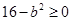 时,解得
时,解得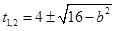 ,这时四边形
,这时四边形 是矩形.
是矩形. ② 当
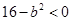 时,
时,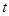 不存在,这时四边形
不存在,这时四边形 不是矩形.
不是矩形. 解法三:如图,过点
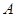 作
作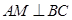 于点
于点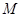 ,
,
在
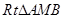 中,
中,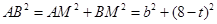
在
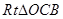 中,
中,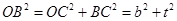
在
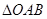 中,当
中,当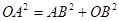 时,
时,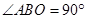 ,
,则四边形
 是矩形.
是矩形.所以
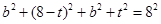
化简得:
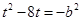
配方得:
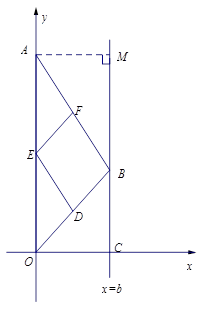
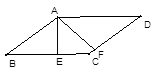
(1)四边形DEFB是平行四边形.利用DE、EF为△OAB的中位线证明平行四边形;
(2)根据DE、EF为△OAB的中位线可知,S△AEF=S△ODE=1/4S△AOB,利用S=S△AOB-S△AEF-S△ODE求S与b的关系式;
(3)当∠ABO=90°时,四边形DEFB是矩形,由Rt△OCB∽Rt△ABO,根据相似比得OB2=OA•BC,由勾股定理得OB2=BC2+OC2,利用b、t分别表示线段的长,列方程求解.
(2)根据DE、EF为△OAB的中位线可知,S△AEF=S△ODE=1/4S△AOB,利用S=S△AOB-S△AEF-S△ODE求S与b的关系式;
(3)当∠ABO=90°时,四边形DEFB是矩形,由Rt△OCB∽Rt△ABO,根据相似比得OB2=OA•BC,由勾股定理得OB2=BC2+OC2,利用b、t分别表示线段的长,列方程求解.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 ,
, ,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则
,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则 应满足什么条件?
应满足什么条件? ,求四边形ABCD的面积.
,求四边形ABCD的面积.
 为
为 边的中点,延长
边的中点,延长 相交于点
相交于点 .
. .
.