Question

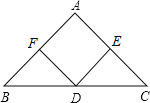
【题目】如图，正方形ABCD中，P在对角线BD上，E在CB的延长线上，且PE=PC，过点P作PF⊥AE于F，直线PF分别交AB、CD于G、H，

（1）求证：DH=AG+BE；

（2）若BE=1，AB=3，求PE的长．

Answer 1

【答案】（1）证明见解析；（2） .

【解析】

试题

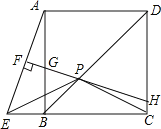
（1）如图，在DC上截取DM=BE，连接AM，则由已知可证△ABE≌ADM，再证四边形AGHM是平行四边形就可得MH=AG，再由DH=MH+DM=AG+BE即可得到结论；

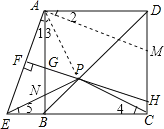
（2）如图，连接AP，由已知可证：△ABP≌△CBP，得到PA=PC，∠3=∠4，结合PC=PE可证得PA=PE，∠3=∠5；再由∠5+∠BNE=∠3+∠ANP=90°，可证∠APE=90°，由此可得△APE是等腰直角三角形；在△ABE中由勾股定理求得AE的长就可解得PE的长.

试题解析：

（1）在DC上截取DM=BE，连接AM，

∵四边形ABCD是正方形，

∴∠ABE=∠ADM=90°，AB=AD，

∵在△ABE和△ADM中： ，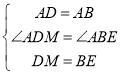

∴△ABE≌ADM，

∴∠1=∠2，

∴∠1+∠BAM=∠2+∠BAM=90°，

∴AM⊥AE．

又∵PF⊥AE于F，

∴AM∥FH，

又∵AB∥CD，

∴四边形AGHM是平行四边形，

∴ AG=MH，

∵ DH=DM+MH，

∴ DH=AG+BE．

（2）连接AP．

∵四边形ABCD是正方形，

∴AB=BC，∠ABP=∠CBP=45°，

∵在△ABP和△CBP中： ，

∴△ABP≌△CBP，

∴PA=PC，∠3=∠4，

∵PE=PC，

∴PA=PE，∠4=∠5，

∴∠3=∠5，

又∵∠ANP=∠ENB，

∴∠3+∠ANP=∠5+∠ENB=90°，

∴AP⊥PE，即△APE是等腰直角三角形，

∵BE=1，AB=3，

∴ AE=，

∴ PE=．