题目内容
如图，四边形ABCD是矩形，AB=3，BC=4，把矩形沿直线AC折叠，点B落在点F处，连接DF，CF与AD相交于点E，求DE的长和△ACE的面积.
由题意，得
，
，
，
∵AD∥BC，
∴
.
∴
.
∴
.
∴
，即
.
设
，则
，
，
在Rt△
中，
.
即
，
解得
. 即
.
∴
.
∴
.
，
，
，
∵AD∥BC，
∴
.∴
.∴
. ∴
，即
. 设
，则
，
，在Rt△
中，
.即
，解得
. 即
. ∴
. ∴
. 在Rt△运用勾股定理计算出DE的长；利用三角形的面积公式求出△ACE的面积.
运用勾股定理计算出DE的长；利用三角形的面积公式求出△ACE的面积.
练习册系列答案
相关题目
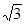≈1.7）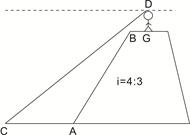
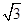，堤高BC=5m，则坡面AB的长度是．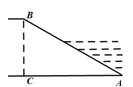
≈1.41，
≈1.73）
，则这个菱形的面积是 。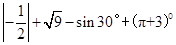
．
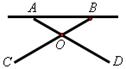
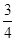，则BC的长是 。