题目内容
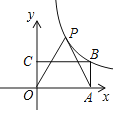
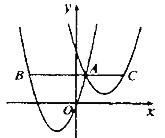
【题目】如图，抛物线
与
交于点
，过点
作
轴的平行线，分别交两条抛物线于点
，则以下结论：①无论取何值，
的值总是正数；②
；③
其中正确结论是（ ）
A. ①②B. ①③C. ②③D. 都正确
【答案】B
【解析】
利用二次函数的性质得到y2的最小值为1，则可对①进行判断；把A点坐标代入y1=a（x+2）2-3中求出a，则可对②进行判断；利用抛物线的对称性计算出AB和AC，则可对③进行判断．
解：∵y2=
+1，
∴y2的最小值为1，所以①正确；
把A（1，3）代入y1=a(x+2)2-3得a(1+2)2-3=3，
∴3a=2，所以②错误；
抛物线y1=a (x+2)2-3的对称轴为直线x=-2，抛物线y2=+1
的对称轴为直线x=3，
∴AB=2×3=6，AC=2×2=4，
∴2AB=3AC，所以③正确．
故答案为①③.故选择B项.
练习册系列答案
相关题目
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱，猕猴桃成熟上市后，她记录了15天的销售数量和销售单价，其中销售单价y（元/千克）与时间第x天（x为整数）的数量关系如图所示，日销量P（千克）与时间第x天（x为整数）的部分对应值如下表所示：
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P（千克） | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）从你学过的函数中，选择合适的函数类型刻画P随x的变化规律，请直接写出P与x的函数关系式及自变量x的取值范围；
（3）在这15天中，哪一天销售额达到最大，最大销售额是多少元；
（4）周老师非常热爱公益事业，若在前5天，周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”，且希望每天的销售额不低于2800元以维持各种开支，求a的最大值.
