题目内容
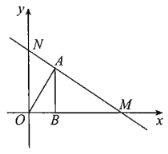
【题目】如图,点M的坐标为![]() ,点A在第一象限,
,点A在第一象限,![]() 轴,垂足为B,
轴,垂足为B,![]() .
.
(1)如果![]() 是等腰三角形,求点A的坐标;
是等腰三角形,求点A的坐标;
(2)设直线MA与y轴交于点N,则是否存在![]() 与
与![]() 相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标是![]() 或
或![]() 或
或![]() ;(2)存在,点A的坐标为
;(2)存在,点A的坐标为![]() 或
或![]() .
.
【解析】
(1)![]() 是等腰三角形的情况有三种:①
是等腰三角形的情况有三种:①![]() ,②
,②![]() ,③
,③![]() ,根据点M的坐标和勾股定理分别求出在不同情况下点A的对应的坐标即可;(2)根据相似三角形的性质,可得
,根据点M的坐标和勾股定理分别求出在不同情况下点A的对应的坐标即可;(2)根据相似三角形的性质,可得![]() ,
,![]() ,根据比例的性质,可得
,根据比例的性质,可得![]() ,
, ![]() ,构建方程组,可解得答案.
,构建方程组,可解得答案.
【解】(1)设![]() ,
,![]() ,①
,①
当![]() 时,则
时,则![]() ,
,
即![]() .②
.②
由①②得, ,
,
解得 ,即
,即![]() .
.
当![]() 时,则
时,则![]() ,即
,即![]() .③
.③
由①③得 ,
,
解得 ,或
,或 ,即
,即![]() .
.
当![]() 时,则
时,则![]() ,即
,即![]() .④
.④
由①④得 ,
,
解得或![]() ,( 舍去),即
,( 舍去),即![]() .
.
综上所述,如果![]() 是等腰三角形,点A的坐标是
是等腰三角形,点A的坐标是![]() 或
或![]() 或
或![]() .
.
(2)存在点A,使以M,O,N为顶点的三角形与![]() 相似.
相似.
当![]() 时.
时.![]() ,故
,故![]() ,
,
则![]() ,
,![]() 0.
0.
直线MN的解析式为![]() ,⑤
,⑤
曲①⑤ ,解得
,解得 ,
,![]() ;
;
当![]() 时.
时.![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
直线MN的解析式为![]() ,⑥
,⑥
由①⑥得 ,解得
,解得![]() .
.![]() .
.
综上所述,当点A的坐标为![]() 或
或![]() 时,
时,![]() 与
与![]() 相似.
相似.

练习册系列答案
相关题目