题目内容
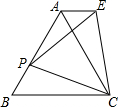 已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.
已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.
证明:∵△ABC与△PCE为等边三角形,
∴AC=BC,EC=PC,∠BCA=∠PCE=60°,
∴∠BCP=∠ACE,
在△BCP和△ACE中,
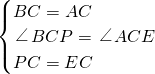 ,
,
∴△CBP≌△CAE(SAS),
∴∠CAE=∠B=60゜=∠ACB,
∴AE∥BC.
分析:由△ABC与△PCE为等边三角形,可证得△CBP≌△CAE(SAS),则可得∠CAE=∠B=60゜=∠ACB,继而证得AE∥BC.
点评:此题考查了全等三角形的判定与性质、等边三角形的性质以及平行线的判定.此题难度不大,注意掌握数形结合思想的应用.
∴AC=BC,EC=PC,∠BCA=∠PCE=60°,
∴∠BCP=∠ACE,
在△BCP和△ACE中,
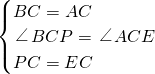 ,
,∴△CBP≌△CAE(SAS),
∴∠CAE=∠B=60゜=∠ACB,
∴AE∥BC.
分析:由△ABC与△PCE为等边三角形,可证得△CBP≌△CAE(SAS),则可得∠CAE=∠B=60゜=∠ACB,继而证得AE∥BC.
点评:此题考查了全等三角形的判定与性质、等边三角形的性质以及平行线的判定.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
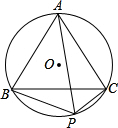 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是

 已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为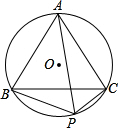 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点. 上任一点.
上任一点.