题目内容
二次函数y=ax2的图象向左平移2个单位，向下平移3个单位，所得新函数表达式为
- A.y=a（x-2）2+3
- B.y=a（x-2）2-3
- C.y=a（x+2）2+3
- D.y=a（x+2）2-3
D
分析：根据向左平移横坐标减，向下平移纵坐标减求出新函数的顶点坐标，然后利用顶点式形式写出即可．
解答：∵二次函数y=ax2的图象向左平移2个单位，向下平移3个单位，
∴新函数的顶点坐标为（-2，-3），
∴新函数表达式为y=a（x+2）2-3．
故选D．
点评：本题考查了二次函数图象与几何变换，利用顶点的变换确定抛物线的变换更加简便．
分析：根据向左平移横坐标减，向下平移纵坐标减求出新函数的顶点坐标，然后利用顶点式形式写出即可．
解答：∵二次函数y=ax2的图象向左平移2个单位，向下平移3个单位，
∴新函数的顶点坐标为（-2，-3），
∴新函数表达式为y=a（x+2）2-3．
故选D．
点评：本题考查了二次函数图象与几何变换，利用顶点的变换确定抛物线的变换更加简便．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知点（a，8）在二次函数y=ax2的图象上，则a的值是（ ）
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、±
|
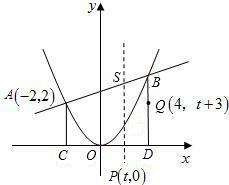Q（4，t+3）分别为线段CD和BD上的动点，过点P且平行于y轴的直线与抛物线和直线分别交于R，S．
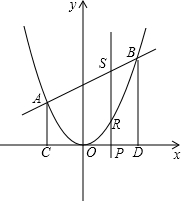点，过点P且平行于y轴的直线与抛物线和直线分别交于R，S．