题目内容
2.在Rt△ABC中,∠C=90°,AB=3BC,则sinB=$\frac{2\sqrt{2}}{3}$,cosB=$\frac{1}{3}$.分析 设BC为x,根据题意用x表示出AB,根据勾股定理求出BC,运用正弦和余弦的定义解答即可.
解答 解:设BC为x,则AB=3x,
由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{2}$x,
sinB=$\frac{AC}{AB}$=$\frac{2\sqrt{2}}{3}$,
cosB=$\frac{BC}{AB}$=$\frac{1}{3}$,
故答案为:$\frac{2\sqrt{2}}{3}$;$\frac{1}{3}$.
点评 本题考查的是锐角三角函数的定义和勾股定理的应用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
17. 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=2,则t的值是( )
如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=2,则t的值是( )
 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=2,则t的值是( )
如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=2,则t的值是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
14.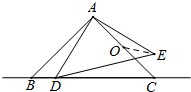 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
 如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.
如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.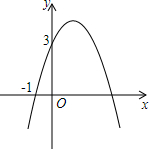 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).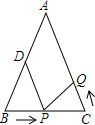 如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.