Question

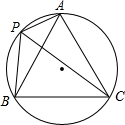如图，点A、P、B、C在⊙O上，∠APB=120°，．
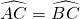（1）判断△ABC形状并说明理由；
（2）如果⊙O的半径是2，sin∠ACP=，求AP的长度；
（3）线段PA、PB、PC之间存在怎样的数量关系，证明你的结论．

Answer 1

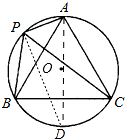解：（1）△ABC是等边三角形．
证明：∵∠ACB=180°-∠APB=180°-120°=60°
∵
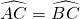
∴AC=BC
∴△ABC是等边三角形；

（2）作直径AD，连接PD．
∵∠D=∠ACP
∴sinD=sin∠ACP==
∴AP=AD=1．

（3）猜想：PC=BP+AP
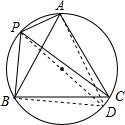
证明：作直径PD，连接AD，BD．
设∠ACP=α，则∠ADP=∠ACP=α，∠BDP=∠ADB-∠ADP=60°-α．
∵PD是直径，
∴∠PBD=90°，
∴PB=PD•sin∠BDP=2R•sin（60°-α）
=2R•（sin60°•cosα-cos60°•sinα）
=2R•（•cosα-sinα）
=R•cosα-R•sinα…①，
同理，PC=2R•sin（60°+α）=R•cosα+R•sinα…②，
PA=R•sinα…③
②-①得：PC-PB=2R•sinα=PA．
∴CP=BP+AP．
分析：（1）此题先根据∠APB=120°，得出：∠ACB的值，再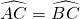，得出AC=BC，即可得出△ABC是等边三角形；
（2）先作直径AD，连接PD，根据等弧所对的圆周角相等，得出∠D=∠ACP，然后得出sinD=sin∠ACP的值，最后得出AP的长度；
（3）延长BP使PD=PA，连接AD，证明△BAD≌△ACP即可解答．
点评：本题主要考查了圆周角定理与全等三角形的判定，利用三角形的全等得出线段相等是解题的关键．