题目内容
若关于x的一元二次方程a(x+m)2=3的两个实数根x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的交点坐标是________.
(4,0)和(0,0)
分析:利用待定系数法求得m、a的值,然后将其代入抛物线y=a(x+m-2)2-3.令y=0,则 (x-3)2-3=0,据此可以求得抛物线y=a(x+m-2)2-3与x轴的交点的横坐标.
(x-3)2-3=0,据此可以求得抛物线y=a(x+m-2)2-3与x轴的交点的横坐标.
解答:∵关于x的一元二次方程3的两个实数根x1=-1,x2=3,
∴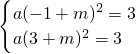 ,
,
解得,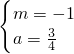 ,
,
则抛物线y=a(x+m-2)2-3= (x-3)2-3,
(x-3)2-3,
令y=0,则 (x-3)2-3=0,
(x-3)2-3=0,
解得,x=4或x=0,
∴抛物线y=a(x+m-2)2-3与x轴的交点坐标是(4,0)和(0,0).
故答案是:(4,0)和(0,0).
点评:本题考查了抛物线与x轴的交点.解答该题时,也可以利用抛物线图象的平移来填空.
分析:利用待定系数法求得m、a的值,然后将其代入抛物线y=a(x+m-2)2-3.令y=0,则
 (x-3)2-3=0,据此可以求得抛物线y=a(x+m-2)2-3与x轴的交点的横坐标.
(x-3)2-3=0,据此可以求得抛物线y=a(x+m-2)2-3与x轴的交点的横坐标.解答:∵关于x的一元二次方程3的两个实数根x1=-1,x2=3,
∴
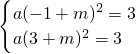 ,
,解得,
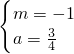 ,
,则抛物线y=a(x+m-2)2-3=
 (x-3)2-3,
(x-3)2-3,令y=0,则
 (x-3)2-3=0,
(x-3)2-3=0,解得,x=4或x=0,
∴抛物线y=a(x+m-2)2-3与x轴的交点坐标是(4,0)和(0,0).
故答案是:(4,0)和(0,0).
点评:本题考查了抛物线与x轴的交点.解答该题时,也可以利用抛物线图象的平移来填空.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目