题目内容

如图，点A₁、A₂，B₁、B₂，C₁、C₂分别是△ABC的边BC、CA、AB的三等分点，且△ABC的周长为18，则六边形A₁A₂B₁B₂C₁C₂的周长为

A.
6
B.
54
C.
36
D.
12

D
分析：根据题意得A₁A₂+B₁B₂+C₁C₂=△ABC周长的 $\text{[math]}$ ，B₂C₂：BC=1：3，A₁C₁：AC=1：3，A₂B₁：AB=1：3，则B₂C₂+A₁C₁+A₂B₁=△ABC周长的 $\text{[math]}$ ，从而得出六边形的周长等于三角形ABC周长的 $\text{[math]}$ ．
解答：∵点A₁、A₂，B₁、B₂，C₁、C₂分别是△ABC的边BC、CA、AB的三等分点，
∴A₁A₂+B₁B₂+C₁C₂=△ABC周长的 $\text{[math]}$ ，
B₂C₁：BC=1：3，A₁C₁：AC=1：3，A₂B₁：AB=1：3，
∴B₂C₁+A₁C₂+A₂B₁=△ABC周长的 $\text{[math]}$ ，
∵ABC的周长为18，
∴A₁A₂+B₁B₂+C₁C₂=6，B₂C₁+A₁C₂+A₂B₁=6，
∴六边形A₁A₂B₁B₂C₁C₂的周长为6+6=12．
故选D．
点评：本题考查的知识点：三等分点，连接三角形三等分点的线段平行于三角形的第三边．

练习册系列答案

期末红100系列答案

冠军练加考课时作业单元期中期末检测系列答案

风向标系列答案

金色阳光AB卷系列答案

高分计划一卷通系列答案

单元测评卷精彩考评七年级下数学延边教育出版社系列答案

王朝霞期末真题精编系列答案

各地期末名卷精选系列答案

导与练初中同步练案系列答案

满分夺冠期末测试卷系列答案

相关题目

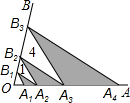如图，点A₁，A₂，A₃，A₄在射线OA上，点B₁，B₂，B₃在射线OB上，且A₁B₁∥A₂B₂∥A₃B₃，A₂B₁∥A₃B₂∥A₄B₃．若△A₂B₁B₂，△A₃B₂B₃的面积分别为1，4，则图中三个阴影三角形面积之和为

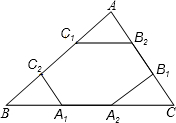如图，点A₁、A₂，B₁、B₂，C₁、C₂分别是△ABC的边BC、CA、AB的三等分点，若△ABC的周长为L，则六边形A₁A₂B₁B₂C₁C₂的周长为（　　）

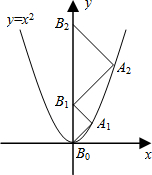如图，点A₁、A₂、A₃、…、A_n在抛物线y=x²图象点B₁、B₂、B₃、…、B_n在y轴上，若△A₁B₀B₁、△A₂B₁B₂、…、△A_nB_n-1B_n都为等腰直角三角形（点B₀是坐标原点），则△A₂₀₁₂B₂₀₁₁B₂₀₁₂的腰长=

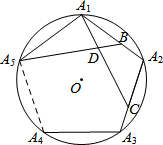如图，点A₁、A₂、A₃、…、A_n在抛物线y=x²图象上，点B₁、B₂、B₃、…、B_n在y轴上，若△A₁B₀B₁、△A₂B₁B₂、…、△A_nB_n-1B_n都为等腰直角三角形（点B₀是坐标原点），则△A₂₀₁₃B₂₀₁₂B₂₀₁₃的腰长=

（2013•南京二模）如图，点A₁、A₂、A₃、A₄、A₅在⊙O上，且

，B、C分别是A₁A₂、A₂A₃上两点，A₁B=A₂C，A₅B与A₁C相交于点D，则∠A₅DC的度数为