题目内容
已知 x1、x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
(1)求k的取值范围.
(2)是否存在实数k,使(2x1-x2)(x1-2x2)=-
成立?若存在求出k的值;若不存在,请说明理由.
(1)求k的取值范围.
(2)是否存在实数k,使(2x1-x2)(x1-2x2)=-
| 3 | 2 |
分析:(1)根据已知可知,方程有两个实数根,那么△≥0,解不等式即可;
(2)由于方程有两个实数根,那么根据根与系数的关系可得x1+x2=1,x1x2=
,然后把x1+x2、x1x2代入(2x1-x2)(x1-2x2)=-
中,进而可求k的值.
(2)由于方程有两个实数根,那么根据根与系数的关系可得x1+x2=1,x1x2=
| k+1 |
| 4k |
| 3 |
| 2 |
解答:解:(1)∵x1、x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,
∴△=b2-4ac=16k2-4×4k(k+1)=-16k≥0,且4k≠0,
解得k<0;
(2)∵x1、x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,
∴x1+x2=1,x1x2=
,
∴(2x1-x2)(x1-2x2)=2x12-4x1x2-x1x2+2x22=2(x1+x2)2-9x1x2=2×12-9×
=2-
,
若2-
=-
成立,
解上述方程得,k=
,
∵(1)中k<0,(2)中k=
,
∴矛盾,
∴不存在这样k的值.
∴△=b2-4ac=16k2-4×4k(k+1)=-16k≥0,且4k≠0,
解得k<0;
(2)∵x1、x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,
∴x1+x2=1,x1x2=
| k+1 |
| 4k |
∴(2x1-x2)(x1-2x2)=2x12-4x1x2-x1x2+2x22=2(x1+x2)2-9x1x2=2×12-9×
| k+1 |
| 4k |
| 9(k+1) |
| 4k |
若2-
| 9(k+1) |
| 4k |
| 3 |
| 2 |
解上述方程得,k=
| 9 |
| 5 |
∵(1)中k<0,(2)中k=
| 9 |
| 5 |
∴矛盾,
∴不存在这样k的值.
点评:本题考查了根的判别式、根与系数的关系,解题的关键是注意数值的正负不等号的变化关系、以及完全平方公式的使用.

练习册系列答案
相关题目
 ,x1•x2=
,x1•x2= ,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题: ,求m的值和此时方程的两根.
,求m的值和此时方程的两根.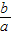 ,x1•x2=
,x1•x2= ,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题: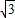 ,求m的值和此时方程的两根.
,求m的值和此时方程的两根.