题目内容
如图,抛物线y=-x2+2nx+n2-9(n为常数)经过坐标原点和x轴上另一点C,顶点在第一象限.
(1)确定抛物线所对应的函数关系式,并写出顶点坐标;
(2)在四边形OABC内有一矩形MNPQ,点M,N分别在OA,BC上,A点坐标为(2,8)B点坐标为(4,8),点Q,P在x轴上.当MN为多少时,矩形MNPQ的面积最大,最大面积是多少?

(1)确定抛物线所对应的函数关系式,并写出顶点坐标;
(2)在四边形OABC内有一矩形MNPQ,点M,N分别在OA,BC上,A点坐标为(2,8)B点坐标为(4,8),点Q,P在x轴上.当MN为多少时,矩形MNPQ的面积最大,最大面积是多少?

(1)∵抛物线过(0,0)点.
∴n2-9=0(1分)
∴n=±3,(2分)
∵顶点在第一象限,
∴-
=n>0且
=
=n2>0(不写不扣分),
∴n=3(3分)
∴抛物线y=-x2+6x(4分)
顶点坐标为(3,9).(5分)
(2)如图所示,作AH⊥x轴于H.
设M点的坐标为(x,y)
∴△OMQ∽△OAH,
∴
=
(7分)
∴
=
,
∴y=4x(8分)
由抛物线的对称性可知:QP=MN=6-2x.(9分)
∴SMNPQ=4x(6-2x)=-8x2+24x(10分)
∴当x=-
=-
=
时,(11分)MN=6-
×2=3时,SMNPQ最大=-8×
+24×
=18,
答:MN等于3时,矩形MNPQ的最大面积是18.(12分)

∴n2-9=0(1分)
∴n=±3,(2分)
∵顶点在第一象限,
∴-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| -4n2 |
| -4 |
∴n=3(3分)
∴抛物线y=-x2+6x(4分)
顶点坐标为(3,9).(5分)
(2)如图所示,作AH⊥x轴于H.
设M点的坐标为(x,y)
∴△OMQ∽△OAH,
∴
| OQ |
| OH |
| MQ |
| AH |
∴
| x |
| 2 |
| y |
| 8 |
∴y=4x(8分)
由抛物线的对称性可知:QP=MN=6-2x.(9分)
∴SMNPQ=4x(6-2x)=-8x2+24x(10分)
∴当x=-
| b |
| 2a |
| 24 |
| -16 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
答:MN等于3时,矩形MNPQ的最大面积是18.(12分)


练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
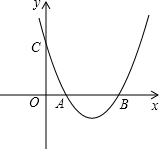 交于点C(0,2).
交于点C(0,2).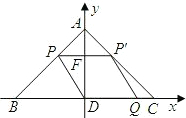 向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.

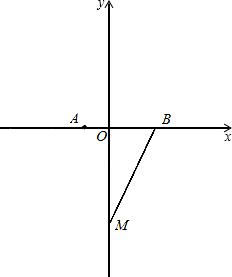 点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
点M在y轴的负半轴上,且|AB|=6,cos∠OBM=