题目内容
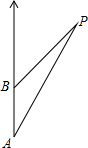已知如图海岛P的周围18千米的范围内有危险，一艘海轮在点A处测得海岛P在北偏东30°的方向，向正北航行12千米到达点B处，又测得海岛P在北偏东45°的方向，如果海轮不改变航向，继续向北航行有没有危险？分析：过点P作PC⊥AB于点C，则直角△PCD和直角△PCA有公共边PC，在两个直角三角形中，求得AD的长，与18海里比较，确定货轮继续向北航行，有无触礁危险．
解答：解：过点P作PC⊥AC于点C．
在直角△PCD中，∠PBC=45°，则直角△PBC是等腰直角三角形，则PC=BC．
在直角△ABD中，∠PAC=30°，
∴AC=
•PC．
∵AB=AC-BC，
∴12=
PC-PC，
∴PC=
=6（
+1）＜18海里．
答：该船继续向北航行有触礁的危险．
在直角△PCD中，∠PBC=45°，则直角△PBC是等腰直角三角形，则PC=BC．
在直角△ABD中，∠PAC=30°，
∴AC=
| 3 |
∵AB=AC-BC，
∴12=
| 3 |
∴PC=
| 12 | ||
|
| 3 |
答：该船继续向北航行有触礁的危险．
点评：本题主要考查了三角形的计算，一般的三角形可以通过作高线转化为解直角三角形的计算，计算时首先计算直角三角形的公共边是常用的思路．
练习册系列答案
相关题目
已知如图海岛P的周围18千米的范围内有危险，一艘海轮在点A处测得海岛P在北偏东30°的方向，向正北航行12千米到达点B处，又测得海岛P在北偏东45°的方向，如果海轮不改变航向，继续向北航行有没有危险？