Question

【题目】在中，点为上一点，点为上一点，且．

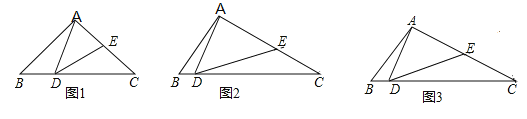
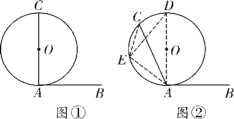
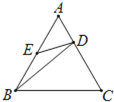
(1)如图1，若，求证：；

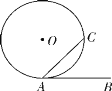
(2)如图2，若，求证：；

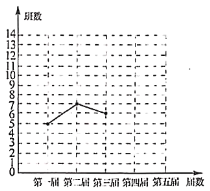
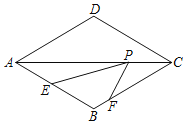
(3) 如图3，在(2)的条件下，若，且，，直接写出线段的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）AB= ．

【解析】

（1）证明△ABD∽△DCE即可解决问题．
（2）如图2中，作CH∥AD交DE的延长线于H．首先证明CE=CH，再证明△BAD∽△HDC即可解决问题．
（3）如图3中，作CH∥AD交DE的延长线于H，作CG⊥EH于G．证明△ECH是等腰直角三角形，解直角三角形求出CD，DH，AD，再利用相似三角形的性质即可解决问题．

（1）证明：如图1中，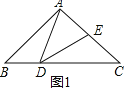

∵AB=AC，
∴∠B=∠C，
∵∠ADC=∠B+∠DAB=∠ADE+∠EDC，∠ADE=∠B，
∴∠EDC=∠BAD，
∴△ABD∽△DCE，
∴，
∴ ．
（2）证明：如图2中，作CH∥AD交DE的延长线于H．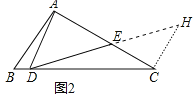

∵AD=AE，
∴∠ADE=∠AED，
∵AD∥CH，
∴∠H=∠ADE，
∵∠AED=∠CEH，
∴∠H=∠CEH，
∴CE=CH，
∵∠ADE=∠B，∠ADE=∠H，
∴∠B=∠H，
∵∠HDC=∠BAD，
∴△BAD∽△HDC，
∴ ，
∴ ，
∴ ．
（3）解：如图3中，作CH∥AD交DE的延长线于H，作CG⊥EH于G．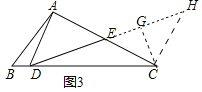

∵∠DAC=90°，AD=AE，
∴∠ADE=∠AED=∠H=∠CEH=45°，
∴EC=CH=4，∠ECH=90°，
∵CG⊥EH，
∴EH=4，EG=CG=GH=2，
∵sin∠CDE=，
∴CD=2 ，
∴DE=EG=2，DH=6，
∴AD=DE=2，
∵△BAD∽△HDC，
∴，
∴ ，
∴AB= ．