Question

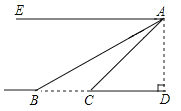
【题目】如图，抛物线y＝x2+bx+c与x轴的交点为A（﹣1，0），B（3，0），与y轴交于点N，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接CP、DP，过点P作CP的垂线与y轴交于点E．

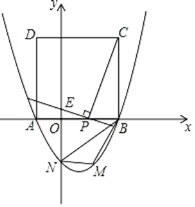
（1）求该抛物线的函数关系表达式；

（2）当CP+DP的值最小时，求E点的坐标；

（3）在第四象限的抛物线上任取一点M，连接MN、MB，是否存在点M使得△MNB为直角三角形；若存在，求出此时点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线函数关系表达式为y＝x2﹣2x﹣3；（2）点E（0，2）；（3）点M的坐标为 或（1，﹣4）．

【解析】

（1）把A、B两点坐标代入抛物线表达式，即可求解；

（2）如图，过点C作关于x轴的对称点H（3，﹣4），连接HD交x轴于点P，交y轴于点E，CP+DP＝PH+PD＝DH为最小，即可求解；

（3）分∠BNM为直角、∠NMB为直角两种情况，分别求解即可．

（1）∵抛物线y＝x2+bx+c经过A（﹣1，0），B（3，0），

把A、B两点坐标代入上式，，解得，

故抛物线函数关系表达式为y＝x2﹣2x﹣3；

（2）如图，过点C作关于x轴的对称点H（3，﹣4），连接HD交x轴于点P，交y轴于点E，

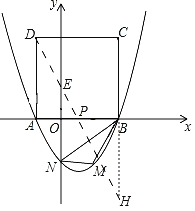
则CP+DP＝PH+PD＝DH为最小，

设直线DH的表达式为：y＝kx+t，则，解得，

故直线DH的表达式为：y＝﹣2x+2，

令x＝0，则y＝2，

故点E（0，2）；

（3）从图上可以看出，∠NBM≠90°；

①当∠BNM为直角时，

∵OB＝OC，

∴∠ONB＝45°，

则NM与y轴负半轴的夹角为45°，

而点N（0，﹣3），设抛物线的顶点为K，则其坐标为（1，﹣4），

从N、K的坐标看，NK与y轴负半轴的夹角为45°，

故点K与点M重合，故点M（1，﹣4）；

②当∠NMB为直角时，

∵∠NOB＝90°，

∴O、B、M、N四点共圆，

设该圆的圆心为R，R是NB的中点，故R的坐标为（，﹣），

设圆的半径为r，则r＝NB＝；

设点M（x，y），y＝x2﹣2x﹣3，

则RM＝r，即（x﹣）2+（y+）2＝（）2，

整理得：（x﹣3）+y（x﹣2）＝0，

即（x﹣3）[1+（1+x）（x﹣2）]＝0，

解得：x＝或（舍去）或3（舍去），

故点M的坐标为（，﹣）；

综上，点M的坐标为（，﹣）或（1，﹣4）．