题目内容
如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= DC,连结
DC,连结 并延长交
并延长交 的延长线于点
的延长线于点

(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
(1)答案见试题解析;(2)10.
解析试题分析:(1)利用正方形的性质,可得∠A=∠D,根据已知可得 ,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
(2)根据平行线分线段成比例定理,可得CG的长,即可求得BG的长.
试题解析:(1)证明:∵ABCD为正方形,∴AD=AB=DC=BC,∠A=∠D=90°,∵AE=ED,∴ ,∵DF=
,∵DF= DC,∴
DC,∴ ,∴
,∴ ,∴△ABE∽△DEF;
,∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,∴ED∥BG,∴ ,又∵DF=
,又∵DF= DC,正方形的边长为4,∴ED=2,CG=6,∴BG=BC+CG=10.
DC,正方形的边长为4,∴ED=2,CG=6,∴BG=BC+CG=10.
考点:1.相似三角形的判定;2.正方形的性质;3.平行线分线段成比例.

练习册系列答案
相关题目
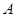 的坐标为
的坐标为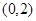 ,点
,点 在
在 轴上,
轴上, 是线段
是线段 的中点.将线段
的中点.将线段 绕着点
绕着点 顺时针方向旋转
顺时针方向旋转 ,得到线段
,得到线段 ,连结
,连结 、
、 .
.
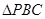 的形状,并简要说明理由;
的形状,并简要说明理由; 时,试问:以
时,试问:以 、
、 为顶点的四边形能否为平行四边形?若能,求出相应的
为顶点的四边形能否为平行四边形?若能,求出相应的 的值?若不能,请说明理由;
的值?若不能,请说明理由; 与
与 相似?
相似?
 .
.
 .
.
 的值 .
的值 .

