题目内容
 如图,OM、OP、ON分别是∠AOB、∠AOC和∠BOC的平分线,则下列各式能成立的是( )
如图,OM、OP、ON分别是∠AOB、∠AOC和∠BOC的平分线,则下列各式能成立的是( )分析:根据角平分线定义得出∠AOP=
∠AOC,∠BOM=
∠AOB,∠BON=
∠BOC,求出∠MON=∠BON+∠BOM=
∠AOC,即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OM、OP、ON分别是∠AOB、∠AOC和∠BOC的平分线,
∴∠AOP=∠COP=
∠AOC,∠BOM=
∠AOB,∠BON=
∠BOC,
∴∠MON=∠BON+∠BOM
=
∠BOC+
∠AOB
=
(∠BOC+∠AOB)
=
∠AOC,
∴∠AOP=∠MON,
故选B.
∴∠AOP=∠COP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠BON+∠BOM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴∠AOP=∠MON,
故选B.
点评:本题考查了角平分线定义的应用,主要考查学生的推理能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图,已知OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为
如图,已知OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为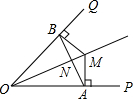 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N. 如图,OM是∠AOB的平分线,OP是∠MOB内的一条射线.已知∠AOP比∠BOP大30°,则∠MOP的度数是
如图,OM是∠AOB的平分线,OP是∠MOB内的一条射线.已知∠AOP比∠BOP大30°,则∠MOP的度数是