题目内容
 已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D、E,连接AD、BD.直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系,若抛物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D、E,连接AD、BD.直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系,若抛物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
①写出顶点B的坐标(用a的代数式表示)________.
②求抛物线的解析式.
③在x轴下方的抛物线上是否存在这样的点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由.
(1,-4a)
分析:①首先求得对称轴,即是点B的横坐标,代入解析式即可求得点B的纵坐标,问题得以解决;
②由△OAD∽△CDB,得出对应线段的比相同求得a的值即可;
③利用三角形相似,等腰三角形的性质,二次函数图象上点的坐标特征以及连点之间的距离解答即可.
解答:①函数y=ax2-2ax-3a的对称轴x=1,代入解析式可得y=-4a,
所以顶点坐标为(1,-4a);
故答案为(1,-4a);
②∵∠BCD=∠AOD=90°,
∠CBD+∠BDC=∠ADO+∠BDC=90°,
即∠CBD=∠ADO,
∴△OAD∽△CDB,
∴ ,
,
∵ax2-2ax-3a=0,可得A(3,0),
又OC=-4a,OD=-3a,CD=-a,CB=1,
∴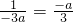 ,
,
∴a2=1,
∵a<0,
∴a=-1,
故抛物线的解析式为:y=-x2+2x+3.
③存在,设P(x,-x2+2x+3),
∵△PAN与△OAD相似,且△OAD为等腰三角形,
∴PN=AN,当x<0(x<-1)时,
-x+3=-(-x2+2x+3),
x1=-2,x2=3(舍去),
∴P(-2,-5),
当x>0(x>3)时,
x-3=-(-x2+2x+3),
x1=0,x2=3(都不合题意舍去),
符合条件的点P为(-2,-5).
点评:此题考查二次函数的顶点坐标,三角形相似的判定与性质,以及二次函数图象上点的坐标特征,是一道较好的题目.
分析:①首先求得对称轴,即是点B的横坐标,代入解析式即可求得点B的纵坐标,问题得以解决;
②由△OAD∽△CDB,得出对应线段的比相同求得a的值即可;
③利用三角形相似,等腰三角形的性质,二次函数图象上点的坐标特征以及连点之间的距离解答即可.
解答:①函数y=ax2-2ax-3a的对称轴x=1,代入解析式可得y=-4a,
所以顶点坐标为(1,-4a);
故答案为(1,-4a);
②∵∠BCD=∠AOD=90°,
∠CBD+∠BDC=∠ADO+∠BDC=90°,
即∠CBD=∠ADO,
∴△OAD∽△CDB,
∴
 ,
,∵ax2-2ax-3a=0,可得A(3,0),
又OC=-4a,OD=-3a,CD=-a,CB=1,
∴
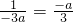 ,
,∴a2=1,
∵a<0,
∴a=-1,
故抛物线的解析式为:y=-x2+2x+3.
③存在,设P(x,-x2+2x+3),

∵△PAN与△OAD相似,且△OAD为等腰三角形,
∴PN=AN,当x<0(x<-1)时,
-x+3=-(-x2+2x+3),
x1=-2,x2=3(舍去),
∴P(-2,-5),
当x>0(x>3)时,
x-3=-(-x2+2x+3),
x1=0,x2=3(都不合题意舍去),
符合条件的点P为(-2,-5).
点评:此题考查二次函数的顶点坐标,三角形相似的判定与性质,以及二次函数图象上点的坐标特征,是一道较好的题目.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
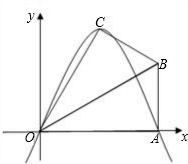 线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
