题目内容
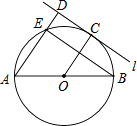
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= . 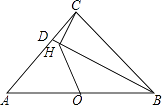
【答案】![]()
【解析】解:在BD上截取BE=CH,连接CO,OE,
∵∠ACB=90°CH⊥BD,
∵AC=BC=3,CD=1,
∴BD= ![]() ,
,
∴△CDH∽△BDC,
∴ ![]() ,
,
∴CH= ![]() ,
,
∵△ACB是等腰直角三角形,点O是AB中点,
∴AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,
∴∠OCH+∠DCH=45°,∠ABD+∠DBC=45°,
∵∠DCH=∠CBD,∴∠OCH=∠ABD,
在△CHO与△BEO中,  ,
,
∴△CHO≌△BEO,
∴OE=OH,∠BOE=∠HOC,
∵OC⊥BO,
∴∠EOH=90°,
即△HOE是等腰直角三角形,
∵EH=BD﹣DH﹣CH= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴OH=EH× ![]() =
= ![]() ,
,
故答案为: ![]() .
.
在BD上截取BE=CH,连接CO,OE,根据相似三角形的性质得到 ![]() ,求得CH=
,求得CH= ![]() ,根据等腰直角三角形的性质得到AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,等量代换得到∠OCH=∠ABD,根据全等三角形的性质得到OE=OH,∠BOE=∠HOC推出△HOE是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.本题考查了相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.
,根据等腰直角三角形的性质得到AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,等量代换得到∠OCH=∠ABD,根据全等三角形的性质得到OE=OH,∠BOE=∠HOC推出△HOE是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.本题考查了相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目