题目内容
 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对边分别为a,b,c.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对边分别为a,b,c.
(1)a=6,b=8,求c及斜边上的高;
(2)a=40,c=41,求b;
(3)b=15,c=25求a;
(4)a:b=3:4,c=15,求b.
解:(1)根据勾股定理,得:c= =10
=10
斜边上的高等于: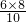 =4.8;
=4.8;
(2)根据勾股定理,得b= =9;
=9;
(3)根据勾股定理,得a= =20;
=20;
(4)由a:b=3:4,根据勾股定理,得a:b:c=3:4:5,
又c=15,则a=9,b=12.
分析:分清要求的是斜边还是直角边,熟练运用勾股定理.
点评:注意:(1)中,直角三角形斜边上的高等于两条直角边的乘积除以斜边;
(2)中,计算的时候运用平方差公式较为简便;
(4)中,根据勾股定理可以求出已知边所占的份数,进一步求解.
 =10
=10斜边上的高等于:
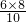 =4.8;
=4.8;(2)根据勾股定理,得b=
 =9;
=9;(3)根据勾股定理,得a=
 =20;
=20;(4)由a:b=3:4,根据勾股定理,得a:b:c=3:4:5,
又c=15,则a=9,b=12.
分析:分清要求的是斜边还是直角边,熟练运用勾股定理.
点评:注意:(1)中,直角三角形斜边上的高等于两条直角边的乘积除以斜边;
(2)中,计算的时候运用平方差公式较为简便;
(4)中,根据勾股定理可以求出已知边所占的份数,进一步求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )