Question

【题目】（1）抛物线经过点A (4，0)，点B (1，－3) ，求该抛物线的解析式；

(2)如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？

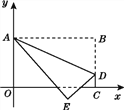
（3）如图，点P（＞0），在轴正半轴上，过点P作平行于轴的直线，分别交抛物线于点A，B，交抛物线于点C，D，求的值.

Answer 1

【答案】（1）;(2) 米;(3)

【解析】试题分析：（1）把A、B的坐标代入抛物线解析式，解方程组，即可求抛物线的解析式；

（2）以池中心为坐标原点，水管为轴建立直角坐标系．设抛物线解析式为 ，把点（3，0）代入，即可求的抛物线的解析式，当x=0时，对应的y的值就是水管的长；

（3）由题意，可得A、B、C、D的坐标，然后求出AB，CD的长，即可得到答案．

试题解析：解：（1）代入点A、B的坐标得： ，解得： ，∴抛物线解析式为： ；

（2）以池中心为坐标原点，水管为轴建立直角坐标系．∵抛物线的顶点坐标为（1，3），

∴设抛物线解析式为，又∵点（3，0）在抛物线上，∴，解得： ，抛物线为．当x=0时y=，故水管应长米；

（3）由题意，可得， ， ， ，∴， ，∴．