Question

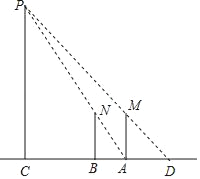
【题目】（探索发现）如图1，△ABC中，点D，E，F分别在边BC，AC，AB上，且AD，BE，CF相交于同一点O．用”S”表示三角形的面积，有S△ABD：S△ACD＝BD：CD，这一结论可通过以下推理得到：过点B作BM⊥AD，交AD延长线于点M，过点C作CN⊥AD于点N，可得S△ABD：S△ACD＝，又可证△BDM～△CDN，∴BM：CN＝BD：CD，∴S△ABD：S△ACD＝BD：CD．由此可得S△BAO：S△BCO＝　 　；S△CAO：S△CBO＝　 　；若D，E，F分别是BC，AC，AB的中点，则S△BFO：S△ABC＝　 　．

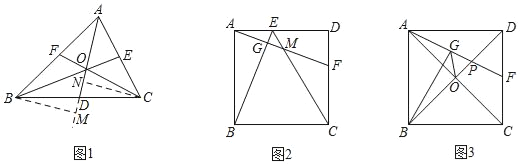
（灵活运用）如图2，正方形ABCD中，点E，F分别在边AD，CD上，连接AF，BE和CE，AF分别交BE，CE于点G，M．

（1）若AE＝DF．判断AF与BE的位置关系与数量关系，并说明理由；

（2）若点E，F分别是边AD，CD的中点，且AB＝4．则四边形EMFD的面积是　 　．

（拓展应用）如图3，正方形ABCD中，AB＝4，对角线AC，BD相交于点O．点F是边CD的中点．AF与BD相交于点P，BG⊥AF于点G，连接OG，请直接写出S△OGP的值．

Answer 1

【答案】[探索发现] AE：EC，AF：BF，1：6．[灵活运用]（1）结论：AF＝BE，AF⊥BE．（2）;[拓展应用] S△GOP＝．

【解析】

【探索发现】利用等高模型，解决问题即可．

【灵活运用】

（1）结论：AF＝BE，AF⊥BE．证明△BAE≌△ADF（SAS）即可解决问题．

（2）根据对称性可知△DME，△DMF，关于直线DM对称，推出S△DME＝S△DMF，由AE＝DE，推出S△AEM＝S△DME＝S△DMF，求出△ADF的面积即可解决问题．

【拓展应用】

由△GPO∽△BPA，推出 即可解决问题．

解：探索发现：由题意：S△BAO：S△BCO＝AE：EC；S△CAO：S△CBO＝AF：BF；若D，E，F分别是BC，AC，AB的中点，则S△BFO：S△ABC＝1：6，

故答案为：AE：EC，AF：BF，1：6．

灵活运用：（1）结论：AF＝BE，AF⊥BE．

理由：如图2中，

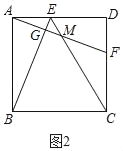
∵四边形ABCD是正方形，

∴AB＝AD，∠BAE＝∠ADF＝90°，

∵AE＝DF，

∴△BAE≌△ADF（SAS），

∴BE＝AF，∠ABE＝∠DAF，

∵∠ABE+∠AEB＝90°，

∴∠DAF+∠AEB＝90°，

∴∠AGE＝90°，

∴AF⊥BE．

（2）如图2﹣1中，连接DM．

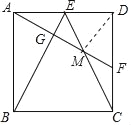
根据对称性可知△DME，△DMF，关于直线DM对称，

∴S△DME＝S△DMF，

∵AE＝DE，

∴S△AEM＝S△DME＝S△DMF，

∵S△ADF＝×4×2＝4，

∴S△AEM＝S△DME＝S△DMF＝，

∴S四边形EMFD＝．

故答案为．

拓展应用：如图3中，

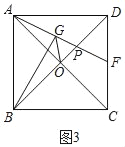
∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD＝4，AC＝BD＝4，OA＝OB＝OD＝OC＝2，

∵DF＝FC，

∴DF＝FC＝2，

∵DF∥AB，

∴，

∴OP：OB＝OP：OA＝1：3，

∵BG⊥PA，AO⊥OB，

∴∠AGB＝∠AOB＝90°，

∵∠OAP+∠APO＝90°，∠PBG+∠BPG＝90°，

∴∠PAO＝∠PBG，

∵∠APO＝∠BPG，

∴△AOP∽△BGP，

∴

∴，∵∠GPO＝∠BPA，

∴△GPO∽△BPA，

∴，

∴S△ABP＝S△ABD＝，

∴S△GOP＝．