题目内容
⊙O1和⊙O2的半径分别为3和2，O1O2=4，A，B为两圆的交点，则AB=________．
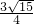
分析：本题可将原图转化成直角三角形求解，连接AO1、AO2形成两个直角三角形，再根据勾股定理即可求出AB的值．
解答：
解：连接O1A，O2A，设O1C=x，则O2C=4-x，∵AC=
=
，∴
=
，解得：x=
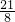，O2C=4-x=
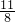；∴AC=
，∴AC=
，∴AB=
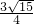．故答案为：
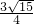．点评：此题考查了相交两圆的性质和直角三角形的性质，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
练习册系列答案
相关题目
17、如图，⊙O1和⊙O2的半径为2和3，连接O1O2，交⊙O2于点P，O1O2=7，若将⊙O1绕点P按顺时针方向以30°/秒的速度旋转一周，请写出⊙O1与⊙O2相切时的旋转时间为