题目内容
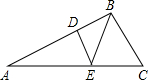如图，D为AB边上一点，DE∥BC交AC于点E，已知DE：BC=4：7，则AD：DB等于
- A.4：7
- B.4：3
- C.3：7
- D.3：4
B
分析：由于DE：BC=4：7，DE∥BC，根据平行线分线段成比例定理可得AD：AB=4：7，那么易求AD：BD=4：3．
解答：∵DE：BC=4：7，
DE∥BC，
∴AD：AB=4：7，
∴AD=
AB，
∴BD=
AB，
∴AD：BD=4：3，
故选B．
点评：本题考查了平行线分线段成比例定理，解题的关键是找出对应线段．
分析：由于DE：BC=4：7，DE∥BC，根据平行线分线段成比例定理可得AD：AB=4：7，那么易求AD：BD=4：3．
解答：∵DE：BC=4：7，
DE∥BC，∴AD：AB=4：7，
∴AD=
AB，∴BD=
AB，∴AD：BD=4：3，
故选B．
点评：本题考查了平行线分线段成比例定理，解题的关键是找出对应线段．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
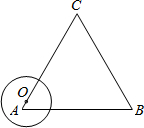如图，△ABC为等边三角形，AB=6，动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周，速度为1个长度单位每秒，以O为圆心、
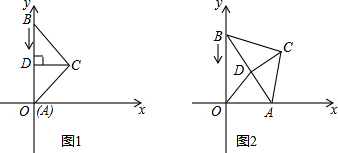沿y轴下滑，并带动△ABC在平面上滑动．如图2，设运动时间表为t秒，当B到达原点时停止运动．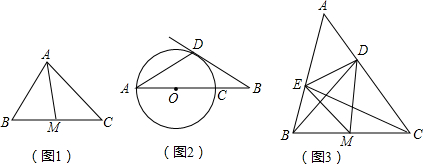
OA交于点F（点D、E、F按顺时针排列），连接DF．设CE=x，OF=y．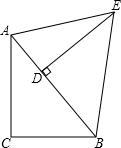
如图所示，在△ABC中，AC=8cm，BC=6cm；在△ABE中，DE为AB边上的高，DE=12cm，△ABE的面积S=60cm2．