题目内容
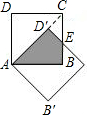
附加题：在正方形ABCD中，P在对角线上，PE⊥BC于点E，PF⊥DC，垂足为F．求证：AP=EF．
证明：分别延长FP、EP交AB于F'，AD于E'，可知四边形BEPF'和FPE′D是正方形，∴PE=PF'=AE'，PF=PE'．
且∠AE'P=∠EPF．
所以△APE'≌△EFP．
即证AP=EF．
分析：根据题意，画出图形，可知，要求EF=AP，可证△APE'≌△EFP．
点评：本题主要考查在正方形中三角形全等的问题，难度一般，要求学生熟练掌握过正方形的对角线上一点分别向相邻两边作垂线则构成正方形．
练习册系列答案
相关题目
附加题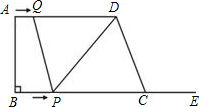
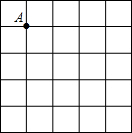（1）从点A出发画一条线段AB，使它的另一端点B在格点（即小正方形的顶点）上，且长度为