题目内容
 如图,△ABC是等腰直角三角形,∠A=90°,AB=4,BD是边AC上的中线.求:
如图,△ABC是等腰直角三角形,∠A=90°,AB=4,BD是边AC上的中线.求:(1)∠ABD的正切值
(2)∠DBC的余弦值.
分析:(1)求出AD的值,关键锐角三角函数求出即可;
(2)过D作DE⊥BC于E,求出DE=EC,根据勾股定理求出DE和BD的值,再求出BE的值,在△BDE中,根据锐角三角函数的定义求出即可.
(2)过D作DE⊥BC于E,求出DE=EC,根据勾股定理求出DE和BD的值,再求出BE的值,在△BDE中,根据锐角三角函数的定义求出即可.
解答:解:(1)Rt△ABD中,∠A=90°AD=2,AB=4,
∴tan∠ABD=
=
.
解:(2)作DE⊥BC于点E,
在△ABD中,由勾股定理得:BD=
=
=2
,
∵等腰直角三角形ACB,
∴∠C=45°,
∵∠DEC=90°,
∴∠CDE=45°=∠C,
∵CD=2,
由勾股定理得:DE=EC=
,
在△BDE中,由勾股定理得:BE=
=3
,
∴∠DBC的余弦值是:
=
=
.
∴tan∠ABD=
| AD |
| AB |
| 1 |
| 2 |
解:(2)作DE⊥BC于点E,

在△ABD中,由勾股定理得:BD=
| AB2+AD2 |
| 42+22 |
| 5 |
∵等腰直角三角形ACB,
∴∠C=45°,
∵∠DEC=90°,
∴∠CDE=45°=∠C,
∵CD=2,
由勾股定理得:DE=EC=
| 2 |
在△BDE中,由勾股定理得:BE=
| BD2-DE2 |
| 2 |
∴∠DBC的余弦值是:
| BE |
| BD |
3
| ||
2
|
3
| ||
| 10 |
点评:本题考查了等腰三角形的性质和判定,等腰直角三角形,勾股定理,锐角三角函数等知识点的应用,解此题的关键是根据勾股定理求出BD、DE、BE的长和理解锐角三角函数定义,通过作此题培养了学生的计算能力,同时也使学生懂得求锐角三角函数值应放在直角三角形中求.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )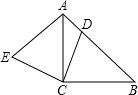 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.