题目内容
函数y= 、y=
、y= (x>0)的图象如图所示.P是y轴上的任意一点,直线x=t(t>0)与两
(x>0)的图象如图所示.P是y轴上的任意一点,直线x=t(t>0)与两 个函数图象分别交于点Q、R,连接PQ、PR.
个函数图象分别交于点Q、R,连接PQ、PR.
(1)当t=3时,求△PQR的面积;
(2)当t从小到大变化时,△PQR的面积是否发生变化,说明理由.
解:(1)∵直线x=t(t>0)与两个函数图象分别交于点Q、R,
∴当t=3时,yQ= =
= ,yR=
,yR= =
= ,
,
∴QR=|yR-yQ|=1,
∴s△PQR= ×1×3=
×1×3= ;
;
(2)当x=t时,Q的纵坐标为 ,R的纵坐标为
,R的纵坐标为 ,
,
∴QR=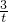 ,
,
∴s△PQR= ×t×
×t×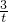 =
= 为一个定值,没变化.
为一个定值,没变化.
分析:(1)△PQR的面积=QR×t÷2;
(2)用t表示出△PQR的面积,看是否为一个定值.
点评:解决本题的关键是正确得到所求三角形的面积的关系式.利用形数结合解决此类问题,是非常有效的方法.
∴当t=3时,yQ=
 =
= ,yR=
,yR= =
= ,
,∴QR=|yR-yQ|=1,
∴s△PQR=
 ×1×3=
×1×3= ;
;(2)当x=t时,Q的纵坐标为
 ,R的纵坐标为
,R的纵坐标为 ,
,∴QR=
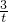 ,
,∴s△PQR=
 ×t×
×t×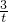 =
= 为一个定值,没变化.
为一个定值,没变化.分析:(1)△PQR的面积=QR×t÷2;
(2)用t表示出△PQR的面积,看是否为一个定值.
点评:解决本题的关键是正确得到所求三角形的面积的关系式.利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| ||
| x |
A、x≤
| ||
B、x>-
| ||
| C、x≠0 | ||
D、x<
|
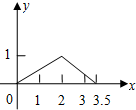
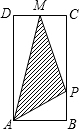 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )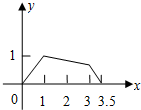


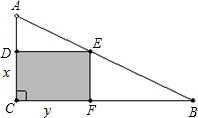 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.