题目内容
已知△ABC中,AB=2
,AC=2,BC边上的高AD=
,则∠ACB=
| 3 |
| 3 |
60或120
60或120
度.分析:分两种情况讨论,(1)∠A为钝角,(2)∠A为钝角,分别画出图形,解三角形,可得∠ACB的度数.
解答:解:(1)当∠A为钝角时,如图①所示:
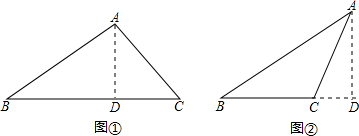
∵AD为高,
∴∠ADB=∠ADC=90°,
∵AC=2,AD=
,
∴在Rt△ACB中,CD=
=1,
∴CD=
AC,
∴∠CAD=30°,
∴∠ACB=90°-∠CAD=60°.
(2)当∠A为锐角时,如图②所示:
∵AB=2,AD=
,
∴CD=
=1,
∴∠CAD=30°,
∴∠ACD=60°,
∴∠ACB=180°-∠ACD=120°.
故答案为:60或120.

∵AD为高,
∴∠ADB=∠ADC=90°,
∵AC=2,AD=
| 3 |
∴在Rt△ACB中,CD=
| AC2-AD2 |
∴CD=
| 1 |
| 2 |
∴∠CAD=30°,
∴∠ACB=90°-∠CAD=60°.
(2)当∠A为锐角时,如图②所示:
∵AB=2,AD=
| 3 |
∴CD=
| AC2-AD2 |
∴∠CAD=30°,
∴∠ACD=60°,
∴∠ACB=180°-∠ACD=120°.
故答案为:60或120.
点评:本题考查了勾股定理的知识,解答本题的关键是掌握勾股定理的表达式,注意分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由. 已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高,
已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高, 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
 如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.
如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.