题目内容
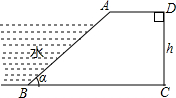
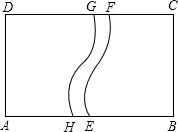
如图，矩形草坪ABCD中，AD=10m，AB=10
m．现需要修一条由两个扇环构成的便道HEFG，扇环的圆心分别是B、D．若便道的宽为1m，则这条便道的面积大约是（ ）（精确到0.1m2）
| 3 |
| A．9.5m2 | B．10.0m2 | C．10.5m2 | D．11.0m2 |
∵四边形ABCD为矩形，
∴△ADB为直角三角形，
又∵AD=10，AB=10
，
∴BD=
=20，
又∵cos∠ADB=
=
，
∴∠ADB=60°．
又矩形对角线互相平分且相等，便道的宽为1m，
所以每个扇环都是圆心角为30°，且外环半径为10.5，内环半径为9.5．
∴每个扇环的面积为
-
=
．
∴当π取3.14时整条便道面积为
×2=10.4666≈10.5m2．
便道面积约为10.5m2．
故选C．
∴△ADB为直角三角形，
又∵AD=10，AB=10
| 3 |
∴BD=
| AD2+AB2 |
又∵cos∠ADB=
| AD |
| BD |
| 1 |
| 2 |
∴∠ADB=60°．
又矩形对角线互相平分且相等，便道的宽为1m，
所以每个扇环都是圆心角为30°，且外环半径为10.5，内环半径为9.5．
∴每个扇环的面积为
| 30×10.52π |
| 360 |
| 30×9.52π |
| 360 |
| 5π |
| 3 |
∴当π取3.14时整条便道面积为
| 5π |
| 3 |
便道面积约为10.5m2．
故选C．
练习册系列答案
相关题目
