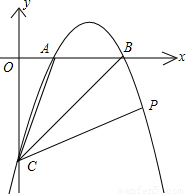
题目内容
如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3(1)求k的值;
(2)求抛物线的解析式;
(3)点P在抛物线上,且∠ACP=45°,求P点的坐标.
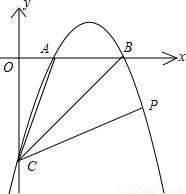
【答案】分析:(1)把点B代入直线,计算即可求出k值;
(2)利用直线解析式求出点C的坐标,再根据△ABC的面积求出AB的长度,然后求出OB的长,再求出OA的长,从而得到点A的坐标,再利用待定系数法求抛物线解析式解答即可;
(3)根据点B、C的坐标求出OB、OC的长度,然后求出∠OCB=∠OBC=45°,BC=3 ,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.
,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.
解答:解:(1)∵直线BC经过B(3,0),
∴3k-3=0,
解得k=1;
(2)由(1)可知直线BC:y=x-3,
当x=0时,y=-3,
所以,C(0,-3),
所以,c=-3,
又∵S△ABC= AB•OC=
AB•OC= AB×3=3,
AB×3=3,
∴AB=2,
∴OA=3-2=1,
∴A(1,0),
由题意,得 ,
,
解得 ,
,
所以,抛物线的解析式为y=-x2+4x-3;
(3)∵B(3,0),C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°,
∴BC=3 ,如图,延长CP交x轴于点Q,
,如图,延长CP交x轴于点Q,
又∵∠ACP=45°,
∴∠OCA=∠BCQ ,
,
在Rt△OAC中,OA=1,OC=3,
∴tan∠OCA= =
= ,AC=
,AC= ,
,
∴tan∠BCQ= ,
,
过B点作BD⊥BC交CQ于点D,则∠QBD=45°,
∴在Rt△BDC中,BD=tan∠BCQ•BC= ×3
×3 =
= ,
,
又∵∠BQD=∠CQA,
∴△BQD∽△CQA,
∴ =
= ,
,
即 =
= =
= ,
,
设BQ=n,则CQ= n,
n,
在Rt△OCQ中,(n+3)2+32=( n)2,
n)2,
整理得,2n2-3n-9=0,
解得,n1=- (负值,舍去),n2=3,
(负值,舍去),n2=3,
即BQ=3,
则OQ=6,
则点Q(6,0),
设直线CP的解析式为y=kx-3,
则6k-3=0,
解得k= ,
,
故直线CP的解析式为y= x-3,
x-3,
联立 ,
,
解得 (为点C坐标,舍去),
(为点C坐标,舍去), .
.
所以点P( ,-
,- ).
).
点评:本题是二次函数综合题型,主要涉及待定系数法求函数解析式(直线解析式,二次函数解析式),三角函数的定义,相似三角形的判定与性质,勾股定理,前两问比较简单,(3)作出辅助线,构造出相似三角形是解题的关键.
(2)利用直线解析式求出点C的坐标,再根据△ABC的面积求出AB的长度,然后求出OB的长,再求出OA的长,从而得到点A的坐标,再利用待定系数法求抛物线解析式解答即可;
(3)根据点B、C的坐标求出OB、OC的长度,然后求出∠OCB=∠OBC=45°,BC=3
 ,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.
,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.解答:解:(1)∵直线BC经过B(3,0),
∴3k-3=0,
解得k=1;
(2)由(1)可知直线BC:y=x-3,
当x=0时,y=-3,
所以,C(0,-3),
所以,c=-3,
又∵S△ABC=
 AB•OC=
AB•OC= AB×3=3,
AB×3=3,∴AB=2,
∴OA=3-2=1,
∴A(1,0),
由题意,得
 ,
,解得
 ,
,所以,抛物线的解析式为y=-x2+4x-3;
(3)∵B(3,0),C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°,
∴BC=3
 ,如图,延长CP交x轴于点Q,
,如图,延长CP交x轴于点Q,又∵∠ACP=45°,
∴∠OCA=∠BCQ
 ,
,在Rt△OAC中,OA=1,OC=3,
∴tan∠OCA=
 =
= ,AC=
,AC= ,
,∴tan∠BCQ=
 ,
,过B点作BD⊥BC交CQ于点D,则∠QBD=45°,
∴在Rt△BDC中,BD=tan∠BCQ•BC=
 ×3
×3 =
= ,
,又∵∠BQD=∠CQA,
∴△BQD∽△CQA,
∴
 =
= ,
,即
 =
= =
= ,
,设BQ=n,则CQ=
 n,
n,在Rt△OCQ中,(n+3)2+32=(
 n)2,
n)2,整理得,2n2-3n-9=0,
解得,n1=-
 (负值,舍去),n2=3,
(负值,舍去),n2=3,即BQ=3,
则OQ=6,
则点Q(6,0),
设直线CP的解析式为y=kx-3,
则6k-3=0,
解得k=
 ,
,故直线CP的解析式为y=
 x-3,
x-3,联立
 ,
,解得
 (为点C坐标,舍去),
(为点C坐标,舍去), .
.所以点P(
 ,-
,- ).
).点评:本题是二次函数综合题型,主要涉及待定系数法求函数解析式(直线解析式,二次函数解析式),三角函数的定义,相似三角形的判定与性质,勾股定理,前两问比较简单,(3)作出辅助线,构造出相似三角形是解题的关键.

练习册系列答案
相关题目
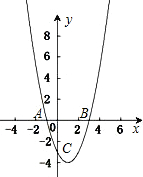 如图,在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C,点C的坐标为(0,-3),且BO=CO.
如图,在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C,点C的坐标为(0,-3),且BO=CO.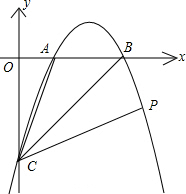 (2012•德化县一模)如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3
(2012•德化县一模)如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3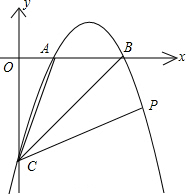 如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3
如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3