题目内容
已知,OM、ON分别是∠AOC,∠BOC的角平分线.
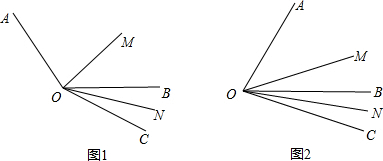
(1)如图1,若∠AOB=120°,∠BOC=30°,则∠MON=
(2)如图1,若∠AOB=120°,∠BOC=β°,能否求出∠MON的度数?若能,求出其值,若不能,试说明理由;
(3)如图2,若∠AOB=α°,∠BOC=β,是否仍然能求出∠MON的度数,若能,求∠MON的度数(用含α或β的式子表示),并从你的求解过程中总结出你发现的规律.

(1)如图1,若∠AOB=120°,∠BOC=30°,则∠MON=
60°
60°
.(2)如图1,若∠AOB=120°,∠BOC=β°,能否求出∠MON的度数?若能,求出其值,若不能,试说明理由;
(3)如图2,若∠AOB=α°,∠BOC=β,是否仍然能求出∠MON的度数,若能,求∠MON的度数(用含α或β的式子表示),并从你的求解过程中总结出你发现的规律.
分析:(1)根据∠AOB=120°,∠BOC=30°,可得∠AOC=∠AOB+∠BOC=120°+30°=150°,再利用OM是∠AOC的平分线,ON是∠BOC的平分线,即可求得答案;
(2)根据∠MON=∠MOC-∠NOC,又利用∠AOB=120°,∠BOC=β°,由(1)可得出答案;
(3)利用(1)(2)的计算方法得出规律即可.
(2)根据∠MON=∠MOC-∠NOC,又利用∠AOB=120°,∠BOC=β°,由(1)可得出答案;
(3)利用(1)(2)的计算方法得出规律即可.
解答:解:(1)∵∠AOB=120°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=120°+30°=150°,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠MON=∠MOC-∠NOC=75°-15°=60°,
(2)当∠AOB=120°,∠BOC=β°时,
∴∠MON=∠MOC-∠NOC=
(120+β)°-
β°=60°;
(3)由(1)(2)可知:
∴∠MON=∠MOC-∠NOC=
(α+β)°-
β°=
α°.
∠MON的度数始终等于∠AOB角度的一半.
∴∠AOC=∠AOB+∠BOC=120°+30°=150°,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOC-∠NOC=75°-15°=60°,
(2)当∠AOB=120°,∠BOC=β°时,
∴∠MON=∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(1)(2)可知:
∴∠MON=∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠MON的度数始终等于∠AOB角度的一半.
点评:此题主要考查角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
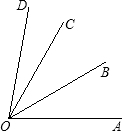 已知:如图,OB、OC分别为定角∠AOD内的两条动射线
已知:如图,OB、OC分别为定角∠AOD内的两条动射线
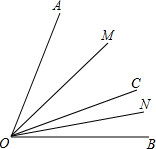 已知,OM和ON分别平分∠AOC和∠BOC.
已知,OM和ON分别平分∠AOC和∠BOC.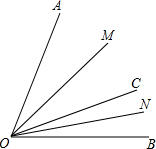 已知,OM和ON分别平分∠AOC和∠BOC.
已知,OM和ON分别平分∠AOC和∠BOC.