题目内容
【题目】已知：如图，在
中， 
，垂足为点
， 
，垂足为点
， 
为
边的中点，连结
、
、
．
（
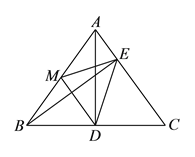
）猜想
的形状，并说明理由．
（
）若
， 
，求
的面积．
【答案】（1） 等腰三角形；（2）
【解析】试题分析：（1）由于AD⊥BC，BE⊥AC，所以△ADB和△ABE是直角三角形，又因为M为AB边的中点，所以ME=MD=
AB，所以△MED为等腰三角形；
（2）由条件知∠EMD=2∠DAC=60°，从而可得等腰三角形DME是边长为2的等边三角形可得到问题答案．
试题解析：（ 
）猜测
为等腰三角形，理由如下．
由题意可得， 
是
斜边上的中线，
∴
，
是
斜边上的中线，
∴
，
∴
，
∴
为等腰三角形．
（
）由（
）中可得： 
， 
，
∴
， 
，
∴
，
，
∴
，
∴在等腰
中， 
，
∴
是等边三角形，边长为
，
∴
．
练习册系列答案
相关题目
