题目内容
抛物线y=a（x+1）2-2的一部分图象如图所示，点P（-3，0）在该抛物线上。
（1）写出抛物线的顶点坐标和对称轴；
（2）确定a的值；
（3）求满足y<0时x的取值范围。
（1）写出抛物线的顶点坐标和对称轴；
（2）确定a的值；
（3）求满足y<0时x的取值范围。
解：（1）顶点坐标是（-1，-2），对称轴是x=-1；
（2）∵抛物线过P（-3，0），
∴当x=-3时，y=0，
∴4a-2=0，
∴
，
（3）∵抛物线的解析式为y=
（x+1）2-2，
当y=0时，
（x+1）2-2=0
∴x1=-3，x2=1，
∴图象与x轴的另一交点坐标为（1，0）
∴ 满足y<0时，x的取值范围是-3<x<1。
（2）∵抛物线过P（-3，0），
∴当x=-3时，y=0，
∴4a-2=0，
∴
，（3）∵抛物线的解析式为y=
（x+1）2-2，当y=0时，
（x+1）2-2=0 ∴x1=-3，x2=1，
∴图象与x轴的另一交点坐标为（1，0）
∴ 满足y<0时，x的取值范围是-3<x<1。
练习册系列答案
学习实践园地系列答案
相关题目
A和C，和x轴的另一个交点为B．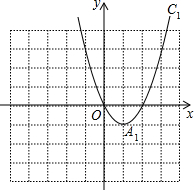
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．