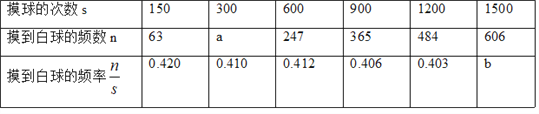
题目内容
【题目】如图,△AOB中,A(-8,0),B(0, ![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,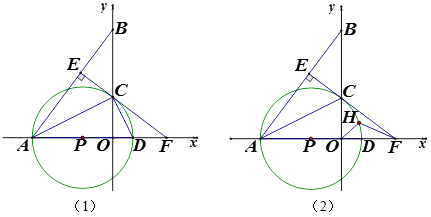
(1)求⊙P的半径;
(2)求证:EF为⊙P的切线;
(3)若点H是 ![]() 上一动点,连接OH、FH,当点P在
上一动点,连接OH、FH,当点P在 ![]() 上运动时,试探究
上运动时,试探究 ![]() 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由.
【答案】
(1)
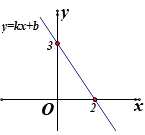
解:依据题意有OA=8,OB= ![]() ,则tan∠BAO=
,则tan∠BAO= ![]() ÷8=
÷8= ![]() .
.
AC是∠BAO的角平分线,则 tan∠BAO= ![]() ,得tan∠CAO=
,得tan∠CAO= ![]() 或-2(舍).
或-2(舍).
已知AO=8,则tan∠CAO= ![]() =
= ![]() ,OC=4。
,OC=4。
显然AD是圆P的直径,CO⊥AD,则易知 ![]() AOC∽
AOC∽ ![]() COD,
COD,
tan∠DCO=∠CAO= ![]() =
= ![]() ,OD=2.
,OD=2.
所以AD=AO+DO=8+2=10.
圆P的半径 10÷2=5
故答案为5.
(2)
证明:连接CP,
∵AP=CP
∴∠PAC=∠PCA
∵AC平分∠OAB
∴∠PAC=∠EAC
∴∠PCA=∠EAC
∴PC//AE
∵CE⊥AB
∴CP⊥EF即EF是⊙P的切线
(3)![]()
是定值, ![]() 连接PH
连接PH
由(1)得AP=PC=PH=5,
∵A(-8,0)
∴OA=8
∴OP=OA-AP=3
在Rt△POC中, ![]()
由射影定理可得 ![]() ,
,
∴OF= ![]()
∴PF=PO+OF= ![]()
∵ ![]()
∴ ![]()
又∵∠HPO=∠FPH
∴△POH∽△PHF
∴ ![]()
当H与D重合时, ![]()
【解析】(1)根据A、B两点的坐标表示出tan∠BAO的值,根据AC是∠BAO的角平分线,进而表示出tan∠CAO的值,已知AO的长度,表示出OC和OD的值,从而求出圆P的半径。(2)连接PC,已知CE⊥AB,证明PC//AB,则必然有PC⊥CE,从而证明EF是圆P的切线。(3)证明△POH∽△PHF,通过相似性,当H与D重合时, ![]() 。
。