题目内容

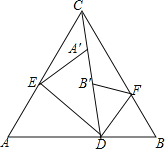
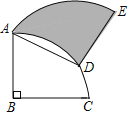
【题目】如图，将半径为4，圆心角为90°的扇形BAC绕A点逆时针旋转60°，点B、C的对应点分别为点D、E且点D刚好在上，则阴影部分的面积为_____．

【答案】+．

【解析】

直接利用旋转的性质结合扇形面积求法以及等边三角形的判定与性质得出S阴影＝S扇形ADE﹣S弓形AD＝S扇形ABC﹣S弓形AD，进而得出答案．

连接BD，过点B作BN⊥AD于点N，

∵将半径为2，圆心角为90°的扇形BAC绕A点逆时针旋转60°，

∴∠BAD＝60°，AB＝AD，

∴△ABD是等边三角形，

∴∠ABD＝60°，

则∠ABN＝30°，

故AN＝1，BN＝，

S阴影＝S扇形ADE﹣S弓形AD＝S扇形ABC﹣S弓形AD

＝ ﹣（﹣×2×）

＝π﹣（π﹣）

＝+．

故答案为： +．

练习册系列答案
相关题目

【题目】胜利中学在一次健康知识竞赛活动中，抽取了一部分学生的测试成绩(成绩均为整数)，整理后绘制成如图所示的频数直方图，根据图示信息，下列描述不正确的是(　　)

A. 抽查了50名学生

B. 成绩在60.5～70.5分范围的频数为2

C. 成绩在70.5～80.5分范围的频数比成绩在60.5～70.5分范围的频数多1

D. 成绩在70.5～80.5分范围的频率为0.8

【题目】如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．

（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．

【题目】每年11月的最后一个星期四是感恩节，小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人．他将调查结果分为如下四类：A类﹣﹣当面致谢；B类﹣﹣打电话；C类﹣﹣发短信息或微信；D类﹣﹣写书信．他将调查结果绘制成如图不完整的扇形统计图和条形统计图：
请你根据图中提供的信息完成下列各题：

（1）补全条形统计图；
（2）在A类的同学中，有3人来自同一班级，其中有1人学过主持．现准备从他们3人中随机抽出两位同学主持感恩节主题班会课，请你用树状图或表格求出抽出的两人都没有学过主持的概率．

【题目】如图，反映了小明从家里到超市的时间与距离之间关系的一幅图。

（1）图中自变量和因变量各是什么？

（2）小明到达超市用了多少时间？超市离家多远？

（3）分别求小明从家里到超市时的平均速度是多少？返回时的平均速度是多少？

【题目】如图，线段AC=6，线段BC=15，点M是AC的中点，在CB上取一点N，使得CN：NB=1：2，求MN的长．

解：∵M是AC的中点，AC=6，

∴MC=______（填线段名称）=______，

又因为CN：NB=1：2，BC=15，

∴CN=______（填线段名称）=______．

∴MN=______（填线段名称）+______（填线段名称）=8

∴MN的长为8．

【题目】在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3，0），将直线y=kx沿y轴向上平移3个单位长度后恰好经过B，C两点．

（1）求直线BC及抛物线的解析式；
（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求点P的坐标；
（3）连接CD，求∠OCA与∠OCD两角和的度数．

【题目】已知三角形的两边分别是2cm和3cm，现从长度分别为1cm、2cm、3cm、4cm、5cm、6cm六根小木棒中随机抽一根，抽到的木棒能作为该三角形第三边的概率是 ．

【题目】如图，等边三角形纸片ABC中，点D在边AB（不包含端点A、B）上运动，连接CD，将∠ADC对折，点A落在直线CD上的点A′处，得到折痕DE；将∠BDC对折，点B落在直线CD上的点B′处，得到折痕DF．

（1）若∠ADC=80°，求∠BDF的度数；

（2）试问∠EDF的大小是否会随着点D的运动而变化？若不变，求出∠EDF的大小；若变化，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网