题目内容
 已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9,AE=2.
已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9,AE=2.
(1)求AD的长;
(2)求 的值.
的值.
解:(1)∵DE∥BC,
∴△AED∽△ACB,
∴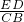 =
= ,
,
∵DE=3,BC=9,AE=2,
∴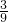 =
= ,
,
∴AC=6,
∵∠C=90°,CB=9,AC=6,
∴AB= =3
=3 ,
,
∵△AED∽△ACB,
∴ =
= ,
,
∴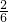 =
=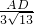 ,
,
AD= ;
;
(2) =
=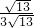 =
= .
.
分析:(1)首先根据DE∥BC可得△AED∽△ACB,进而得到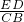 =
= ,再把对应数据代入即可算出AC的长,再利用勾股定理计算出AB的长,然后根据相似三角形的性质可得AD的值;
,再把对应数据代入即可算出AC的长,再利用勾股定理计算出AB的长,然后根据相似三角形的性质可得AD的值;
(2)根据(1)中的计算数据可得答案.
点评:此题主要考查了相似三角形的判定与性质,关键是掌握两个三角形相似也有对应角相等,对应边的比相等.
∴△AED∽△ACB,
∴
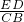 =
= ,
,∵DE=3,BC=9,AE=2,
∴
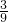 =
= ,
,∴AC=6,
∵∠C=90°,CB=9,AC=6,
∴AB=
 =3
=3 ,
,∵△AED∽△ACB,
∴
 =
= ,
,∴
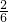 =
=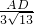 ,
,AD=
 ;
;(2)
 =
=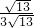 =
= .
.分析:(1)首先根据DE∥BC可得△AED∽△ACB,进而得到
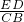 =
= ,再把对应数据代入即可算出AC的长,再利用勾股定理计算出AB的长,然后根据相似三角形的性质可得AD的值;
,再把对应数据代入即可算出AC的长,再利用勾股定理计算出AB的长,然后根据相似三角形的性质可得AD的值;(2)根据(1)中的计算数据可得答案.
点评:此题主要考查了相似三角形的判定与性质,关键是掌握两个三角形相似也有对应角相等,对应边的比相等.

练习册系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,