题目内容
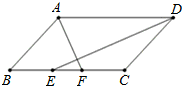 在?ABCD中,AB=5,AD=8,∠BAD、∠ADC的平分线分别交BC于E、F,则EF的长为
在?ABCD中,AB=5,AD=8,∠BAD、∠ADC的平分线分别交BC于E、F,则EF的长为
- A.1
- B.2
- C.3
- D.4
B
分析:由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAF=∠DAF,则BF=AB=5;同理可得,CE=CD=5.而EF=BF+CE-BC,由此可以求出EF长.
解答:∵AF平分∠BAD,
∴∠BAF=∠DAF,
又∵AD∥CB,
∴∠AFB=∠DAF,
∴∠BAF=∠AFB,
则BF=AB=5;
同理可得,CE=CD=5.
∴EF=BF+CE-BC=BF+CE-AD=5+5-8=2.
故选B.
点评:此题主要涉及的知识点:角平分线的定义、平行四边形的性质、平行线的性质,关键注意找出线段之间的关系:EF=BF+CE-BC.
分析:由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAF=∠DAF,则BF=AB=5;同理可得,CE=CD=5.而EF=BF+CE-BC,由此可以求出EF长.
解答:∵AF平分∠BAD,
∴∠BAF=∠DAF,
又∵AD∥CB,
∴∠AFB=∠DAF,
∴∠BAF=∠AFB,

则BF=AB=5;
同理可得,CE=CD=5.
∴EF=BF+CE-BC=BF+CE-AD=5+5-8=2.
故选B.
点评:此题主要涉及的知识点:角平分线的定义、平行四边形的性质、平行线的性质,关键注意找出线段之间的关系:EF=BF+CE-BC.

练习册系列答案
相关题目
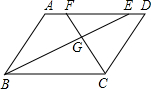 如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )
如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )| A、5:8 | B、25:64 | C、1:4 | D、1:16 |
 如图所示,在?ABCD中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点,EF=1cm,那么对角线BD的长度为
如图所示,在?ABCD中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点,EF=1cm,那么对角线BD的长度为 s的速度沿AB向终点B运动,当它们有一个到达终点时,另一个也随之停止运动,设运动时间为ts.
s的速度沿AB向终点B运动,当它们有一个到达终点时,另一个也随之停止运动,设运动时间为ts.