题目内容
方程9(x+1)2-4(x-1)2=0正确解法是
- A.直接开方得3(x+1)=2(x-1)
- B.化为一般形式13x2+5=0
- C.分解因式得[3(x+1)+2(x-1)][3(x+1)-2(x-1)]=0
- D.直接得x+1=0或x-l=0
C
分析:根据题目的特点,用平方差公式因式分解.
解答:A:直接开平方应得到两个方程:3(x+1)=2(x-1)和3(x+1)=-2(x-1),所以A不正确;
B:化成一般形式应是:5x2+26x+5=0;所以B不正确;
C:方程左边满足平方差形式,可以用平方差公式因式分解为:[3(x+1)+2(x-1)][3(x+1)-2(x-1)]=0,所以C正确.
D:两个完全平方的差为0,不能直接得到两个式子分别是0,只有两个完全平方的和是0,才能直接得到两个式子分别是0,所以D不对.
故选C.
点评:本题考查的是用因式分解法解一元二次方程,根据题目的结构特点,用平方差公式因式分解.
分析:根据题目的特点,用平方差公式因式分解.
解答:A:直接开平方应得到两个方程:3(x+1)=2(x-1)和3(x+1)=-2(x-1),所以A不正确;
B:化成一般形式应是:5x2+26x+5=0;所以B不正确;
C:方程左边满足平方差形式,可以用平方差公式因式分解为:[3(x+1)+2(x-1)][3(x+1)-2(x-1)]=0,所以C正确.
D:两个完全平方的差为0,不能直接得到两个式子分别是0,只有两个完全平方的和是0,才能直接得到两个式子分别是0,所以D不对.
故选C.
点评:本题考查的是用因式分解法解一元二次方程,根据题目的结构特点,用平方差公式因式分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
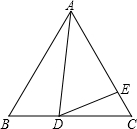 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-