题目内容
在直角坐标系中,将双曲线y=
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )
| 3 |
| x |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
分析:设点(x,y)是双曲线y=
上的点,根据旋转的性质,点(x,y)变为(-x,y),据此求得旋转后双曲线的解析式.
| 3 |
| x |
解答:解:设点(x,y)是双曲线y=
上的点,
∵双曲线y=
绕着坐标原点旋转90°,
∴点(x,y)变为(-x,y),
把(-x,y)代入原解析式,
得y=-
.
故选C.
| 3 |
| x |
∵双曲线y=
| 3 |
| x |
∴点(x,y)变为(-x,y),
把(-x,y)代入原解析式,
得y=-
| 3 |
| x |
故选C.
点评:本题主要考查反比例函数的性质的知识点,解答本题的关键是求出双曲线点的坐标与旋转后点坐标的关系,本题比较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 绕着坐标原点旋转90°后,所得到的双曲线的解析式是
绕着坐标原点旋转90°后,所得到的双曲线的解析式是
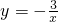
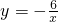
 绕着坐标原点旋转90°后,所得到的双曲线的解析式是( ★ )
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( ★ )


 绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )



 绕着坐标原点旋转90°后,所得到的双曲线的解析式是( ★ )
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( ★ ) C.
C. D.
D.