题目内容
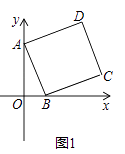
【题目】如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为 ． 
【答案】3
【解析】∵四边形ABCD是矩形，
∴BD=AC，即当AC最小时，BD就最小；
∵在抛物线 
中，顶点（1，3）距离 
轴最近，
∴当点A运动到抛物线的顶点时，AC最短为3，
∴BD的最小值为3.
【考点精析】根据题目的已知条件，利用二次函数的性质和二次函数的最值的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】“端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
（2）列式计算说明，如果顾客在“端午节”当天购买该种粽子超过200元，那么到哪家超市花费更少？
x （单位：元） | 实际在甲超市的花费 （单位：元） | 实际在乙超市的花费 （单位：元） |
0＜x≤200 | x | x |
200＜x≤300 | x | |
x＞300 |
