题目内容
| 104+324 |
| 44+324 |
| 224+324 |
| 164+324 |
| 344+324 |
| 284+324 |
| 464+324 |
| 404+324 |
| 584+324 |
| 524+324 |
考点:有理数无理数的概念与运算
专题:
分析:首先求得a4+324=a4+182=a4+182+36a2-36a2=(a2+18)2-36a2=(a2+18+6a)(a2+18-6a)=[(a+3)2+9][(a-3)2+9],然后代入原式,化简约分即可求得答案.
解答:解:∵a4+324=a4+182=a4+182+36a2-36a2=(a2+18)2-36a2=(a2+18+6a)(a2+18-6a)=[(a+3)2+9][(a-3)2+9],
∴原式=
×
×
×
×
=
=373.
∴原式=
| (132+9)(72+9) |
| (72+9)(12+9) |
| (252+9)(192+9) |
| (192+9)(132+9) |
| (372+9)(312+9) |
| (312+9)(252+9) |
| (492+9)(432+9) |
| (432+9)(372+9) |
| (612+9)(552+9) |
| (552+9)(492+9) |
=
| 612+9 |
| 1+9 |
=373.
点评:此题考查了有理数的概念与运算.此题难度适中,得到a4+324=[(a+3)2+9][(a-3)2+9]是解此题的关键.

练习册系列答案
相关题目
已知α、β是方程x2+2006x+1=0的两个根,则(1+2008α+α2)(1+2008β+β2)的值( )
| A、2006 | B、-4 |
| C、4 | D、-2006 |
 如图,线段AB和线段CD的重合部分CB的长是线段AB长的三分之一,M、N分别是线段AB和线段CD的中点,若AB=12cm,MN=10cm,则线段AD的长为
如图,线段AB和线段CD的重合部分CB的长是线段AB长的三分之一,M、N分别是线段AB和线段CD的中点,若AB=12cm,MN=10cm,则线段AD的长为
 如图,已知正方形ABCD的边长为4,E为CD边上的一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,求EE′的长.
如图,已知正方形ABCD的边长为4,E为CD边上的一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,求EE′的长.
 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是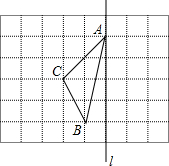 如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.